CÂU CHUYỆN KHOA HỌC 79/c

LẠM BÀN I:
-Không có trực giác, đã không có nhận thức thế giới.
-Tư duy lý trí là con đẻ của trực giác.
-Thế giới thực tại rộng lớn và sâu sắc đến cùng cực, trong khi khả năng trực giác của con người lại hạn định, do đó tư duy lý trí phải hóa thân thành tư duy trừu tượng, lấy suy tư lôgic phi thực chứng làm công cụ để tiếp tục nhận thức thế giới.
-Đó là lý do vì sao khoa học ngày nay bấp bênh đến thế.
-Computer vĩnh viễn là tư duy máy móc, không phải là tư duy trừu tượng của não người. Do đó nó không bao giờ có thể "đẻ ra" một lý thuyết khoa học mới nào.
-Nếu Trái Đất tồn tại đủ lâu thì câu “Chúng ta phải biết; Chúng ta sẽ biết!” sẽ là một chân lý chắc chắn.
-Tình yêu sinh ra từ bản năng sinh tồn và sự thấm thía về nỗi thống khổ của con người. Do đó có thể nói: tình yêu sinh ra Chúa chứ không phải do Chúa sinh ra!
LẠM BÀN II:
-1.Bản chất tận cùng của vật chất và lực? Bản chất vật chất là không gian. Không gian là Tồn Tại. Lực là sự thể hiện của Tồn Tại và sự cố gắng (nỗ lực) thể hiện trạng thái vốn có của tồn tại (tương đối).
2.Nguồn gốc của chuyển động? Đặc tính cơ bản của Tồn Tại là thường biến. Biểu hiện cuối cùng về tính thường biến của vật chất là chuyển động. Chuyển động là vật chất thay đổi trạng thái, vị trí trong không gian.
3.Nguồn gốc sự sống? Biểu hiện về tính đầy đủ của thực tại khách quan là Tồn Tại hình như phân ra làm hai thể tương phản nhau: thụ động - chủ động trong cố gắng tồn tại. Quá trình chuyển hóa từ thụ động sang chủ động trong cố gắng tồn tại là nguồn gốc sinh ra sự sống. Sống là cố gắng sống còn.
4.Tại sao tự nhiên sắp xếp dường như có mục đích? Vì không thể có Hư Vô.
5.Nguồn gốc của những khả năng cảm thụ đơn giản? Một tồn tại không thể tồn tại được nếu xung quanh không biết nó tồn tại. Sự biết đó có được nhờ thông qua tác dụng tương hỗ (tác dụng lực).
6.Nguồn gốc của tư duy thông minh và ngôn ngữ? Trong thiên nhiên hữu hạn, sinh vật phải đấu tranh sinh tồn bằng tiến hóa - thích nghi để sống còn. Tiến hóa - thích nghi là nguồn gốc của tư duy thông minh và ngôn ngữ.
7.Bản chất của tự do ý chí (freewill)? Lựa chọn và được lựa chọn thực hiện phương cách bản thân mình cho là tối ưu để sống còn.
-Câu hỏi hắc búa nhất và cũng là cuối cùng của nhận thức loài người (có thể vĩnh viễn bó tay!): không gian là gì?
-HỌC THUYẾT DARWIN về cơ bản là chân lý chắc chắn, có thể phản biện nhưng không thể bác bỏ được'
-Vũ trụ chuyển hóa và vận động sao cho Tồn Tại được bảo toàn. Đó là tất định!
-Thực tại khách quan là xác định! Chỉ có con người là bất định!
-Toán học, khi thoát ra khỏi phạm vi thực dụng của nó, sẽ trở thành huyễn hoặc và bất toàn. Phải chăng huyễn hoặc và bất toàn lại là bản chất của Vũ Trụ trong miền trừu tượng!?
-Rồi đây, như một tất yếu, nhận thức thế giới thực tại của loài người sẽ đứng dưới bầu trời của duy nhất một học thuyết thống nhất vĩ đại - "HỌC THUYẾT VỀ MỌI THỨ".

LẠM BÀN III:
-Trả lời:

   +Liệu có thể có một “Lý thuyết về mọi thứ” của vật lý không? Có! Nhưng liệu loài người còn tồn tại đến đó để mà biết không?

   +Robots có thể thông minh như con người không? Không, vì thông minh là phải biết sáng tạo ra cái mới hữu dụng.

   +Bản chất vật chất của tinh thần là gì? Là tế bào thần kinh.

   +Máy móc có thể thay thế con người trong dịch thuật không? Không, vì khái niệm luôn đổi mới, có máy móc luôn lạc hậu.

  +Giả thuyết Goldbach là một tiên đề hay một định lý? Tiên đề.

  +Vũ trụ trước Big Bang là gì? Là Hư Vô và điểm Kì Dị. Nhưng Hư Vô là không thể có nên cũng không thể có Big Bang.

  +Tồn tại chăng một lý thuyết dự báo tương lai chính xác? Có mà cũng không.
-Con người sẽ nhận thức được toàn bộ căn nguyên Vũ Trụ. Việc hiểu được 3 bài học tưởng như không sao hiểu được trong thế kỷ 20: Thuyết Tương Đối của Einstein + Nguyên Lý Bất Định của Heisenberg + Bài học về cuộc khủng hoảng trầm trọng trong nền tảng Toán Học đầu thế kỷ 20, là bằng chứng hùng hồn về khả năng nhận thức triệt để Vũ Trụ của con người.
-Khả năng nhận thức là không có giới hạn, nhưng không thể nhận thức được Hư Vô. Nhận thức rằng không thể nhận thức được cũng là nhận thức.
-Không thể tưởng tượng ra Hư Vô.

-Tổng thể Vũ Trụ là suy diễn.
-Không thể dùng toán học để giải thích Vũ Trụ vì nó không phải sự thật.

-----------------------------------------------------------------------
(ĐC sưu tầm trên NET)

 

Kurt Godel, Định lý bất toàn và hệ quả triết học - Phạm Việt Hưng

ĐỊNH LÝ BẤT TOÀN

Phần 1: Thầy Bói Xem Voi

How can a part know the whole? (Blaise Pascal)

Khoa học đang đứng trước hàng loạt câu hỏi thách thức:

-Liệu có thể có một “Lý thuyết về mọi thứ” của vật lý không?

-Robots có thể thông minh như con người không?

-Bản chất vật chất của tinh thần là gì?

-Máy móc có thể thay thế con người trong dịch thuật không?

-Giả thuyết Goldbach là một tiên đề hay một định lý?

-Vũ trụ trước Big Bang là gì?

-Tồn tại chăng một lý thuyết dự báo tương lai chính xác?

Và rất nhiều câu hỏi khác nữa. Mỗi câu hỏi là một thách đố lớn chưa từng có – một “Chiếc Chén Thánh” (The Holy Grail)[1] của khoa học, mà câu trả lời thường dẫn tới sự chia rẽ quan điểm, một bên nói “có”, một bên “không”. Chưa bao giờ khoa học bị rơi vào tình trạng ngã ba đường như hiện nay. Dường như dự cảm được điều đó nên từ lâu Kurt Gödel đã lưu ý: “Ý nghĩa của cuộc sống là ở chỗ biết phân biệt Ước Muốn với Hiện Thực”[2].

Những ai biết rõ lịch sử toán học thế kỷ 20 đều hiểu ngay rằng Gödel ngụ ý nhắc nhở nhân loại không được phép quên bài học thất bại cay đắng của Chương trình Hilbert – một chương trình có tham vọng khám phá ra “Lý thuyết về mọi thứ” của toán học, tức là không hiểu nguyên lý giới hạn của nhận thức mà truyện ngụ ngôn “Thầy Bói Xem Voi” đã nói từ xa xưa.

Thậm chí đến khi Gödel công bố Định lý bất toàn (Theorem of Incompleteness), khẳng định nguyên lý giới hạn của nhận thức dưới dạng toán học, vẫn có nhiều người không muốn thừa nhận nguyên lý này. Đó là lý do để nhiều nhà triết học khoa học Tây phương hiện nay thích nhắc lại tích “Thầy Bói Xem Voi”, như một gợi ý để từ đó đề cập tới Định lý bất toàn nói riêng và vấn đề giới hạn của nhận thức nói chung[3].

1] “Thầy Bói Xem Voi”:

“Thầy Bói Xem Voi” là một truyện ngụ ngôn bằng thơ nhan đề “The Blind Men and the Elephant” (Những anh mù và con Voi), hoặc “Six Men of Indostan” (Sáu anh chàng ở xứ Indostan[4]), của John Godfrey Saxe, một nhà thơ triết lý nổi tiếng người Mỹ thế kỷ 19. Nhưng thực ra tích “Thầy Bói Xem Voi” “đã được ghi chép từ xa xưa trong Kinh Đại Bát Niết Bàn 大般涅槃经 do ngài Đàm Vô Sấm 昙无谶 (Dharmaraksa), pháp sư người Ấn, dịch ra Hoa ngữ , đồng thời cũng đã được ghi chép trong Kinh Trường A Hàm của Phật Giáo”[5].

Thầy Bói Xem Voi

(Sáu anh mù ở xứ Indostan)

John Godfrey Saxe

(1816 – 1887)

Sáu anh mù ở xứ

In-đốt-xtan nóng bỏng

Rủ nhau đi xem Voi

Vì rất ham hiểu biết

Nên thi nhau quan sát

Cho thoả nỗi khát mong

Đầu tiên là anh Nhất

Sờ tấm thân vừa rộng,

Vừa cứng ráp, vừa thô

Miệng oang oang tuyên bố:

“Con Voi, ôi lạy Chúa!

Giống bức tường y chang”

Tiếp đến là anh Nhị,

Sờ ngà Voi, nói lớn:

“Tròn, nhọn, lại mịn trơn?

Kỳ quan này rõ thấy,

Rằng Voi như ngọn giáo,

Đó mới thật là Voi!”

Anh Tam bèn tiến đến

Tay ôm vòi uốn éo,

Ngẫm nghĩ và luận suy,

Rồi tự tin anh nói:

“Con Voi như tôi thấy

Giống con rắn, con trăn”

Đôi bàn tay anh Tứ

Sờ vào chân, háo hức,

“Kỳ lạ nhất của Voi,

Như ta vừa nhận thấy,

Một thân cây thẳng đứng,

Mới giống hình con Voi!”

Rồi đến phiên anh Ngũ,

Sờ tai Voi, tuyên bố:

“Mù nhất chính là ta,

Nhưng nào ai dám cãi,

Rằng Voi như quạt giấy,

Phe phẩy, phẩy gió bay!”!

Cuối cùng là anh Lục,

Dò dẫm, anh vội túm

Chỗ ve vẩy cái đuôi,

Cảm nhận, thốt lên lời:

“Voi như ta đã thấy

Giống y chiếc dây thừng!”

Thế là sáu anh mù

Cãi vã nhau ỏm tỏi ,

Ai cũng cho mình giỏi,

Anh nào cũng hung hăng.

Mỗi anh đúng một phần,

Nhưng đều sai tất cả!

The Blind Men and the Elephant

(Six Men of Indostan)

John Godfrey Saxe

(1816 – 1887)

It was six men of Indostan

To learning much inclined,

Who went to see the Elephant

Though all of them were blind

That each by observation

Might satisfy his mind.

The First approached the Elephant

And happening to fall

Against his broad and sturdy side

At once began to bawl:

“God bless me! But the Elelephant

Is very like a wall”

The Second, feeling of the tusk,

Cried, “Ho! What have we here

So very round & smooth & sharp?

To me ‘tis mighty clear

This wonder of an Elephant

Is very like a spear!”

The Third approached the animal,

And happening to take

The squirming trunk within his hands,

Thus  boldly up and spake :

“I see”, quoth he, “the Elephant

Is very like a s"từ cấm"!”

The Fourth reached out an eager hand,

And felt about the knee.

“What most this wondrous  beast  is like

Is mighty plain”, quoth he;

“ ‘Tis clear enough the Elephant

Is very like a tree!”

The Fifth who chanced to touch the ear,

Said: “E’en the blindest man

Can tell what this resembles most:

Deny the fact who can,

This marvel of an Elephant

Is very like a fan!”

The Sixth the sooner had begun

About the beast to grope,

Than, seizing on the swinging tail

That fell  within his scope ,

“I see”, qouth he, “the Elephant

Is very like a rope!”

And so these men of Indostan

Disputed loud and long,

Each in his own opinion

Exceeding stiff and strong,

Though each was partly in the right

And all were in the wrong!

Ý tưởng của John Saxe thật dễ hiểu: Nhận thức của con người vốn phiến diện và bị giới hạn – nhận thức dù tiến bộ đến mấy cũng chỉ đúng một phần chứ không bao giờ đầy đủ và hoàn thiện.

Nhưng phỏng có ích gì khi nhắc lại triết lý giới hạn của nhận thức trong thời buổi khoa học đang tăng trưởng với tốc độ hàm mũ như hiện nay? Phải chăng đó là một nghịch lý? Sau đây sẽ là câu trả lời.

2] Nghịch lý lớn về nhận thức:

Điều bất ngờ thú vị cần thông báo ngay với độc giả là tích “Thầy Bói Xem Voi” – một chuyện tưởng như đã “biết rồi, khổ lắm, nói mãi” – lại đã và đang tái xuất hiện trên các diễn đàn khoa học tây phương hiện đại với một tầm vóc và bình diện mới! Thật vậy, dưới ánh sáng của những sự kiện khoa học trọng đại nhất trong thế kỷ 20, đặc biệt nhờ những tiến bộ vượt bậc của khoa học computer trong mấy thập kỷ qua, nhân loại đã và đang tái khám phá ra nguyên lý về bản chất giới hạn của nhận thức – một nguyên lý tự nhiên mà tích “Thầy Bói Xem Voi” đã nói từ lâu nhưng dần dần bị lãng quên!Nguyên lý này khẳng định rằng NHẬN THỨC, mặc dù mỗi ngày một tiến hoá, nhưng không bao giờ đạt tới chỗ BIẾT HẾT, BIẾT MỌI THỨ, BIẾT ĐẦY ĐỦ, BIẾT TẬN CÙNG …

Tham vọng biết mọi thứ, xét cho cùng, là … “ngây thơ” – không hiểu hoặc không muốn hiểu một quy luật của nhận thức mà John Saxe đã trình bầy từ lâu dưới dạng thơ ngụ ngôn!

Sự “ngây thơ” đó đáng được thông cảm: Khi khát vọng nhận thức bùng cháy mãnh liệt, con người có xu hướng muốn biết hết, biết tới tận cùng! Đó là một khát vọng chính đáng, tự nhiên theo bản năng, và nhờ đó con người mới khám phá hết bí mật này đến bí mật khác. Đó chính là động lực của tiến hoá. Nếu khát vọng đó đôi khi (hoặc nhiều khi) trở nên thái quá, chẳng qua con người sinh ra vốn bản chất đã hướng ngoại, thích quan sát các đối tượng khách thể bên ngoài hơn là quan sát chính chủ thể nhận thức. Trẻ em thể hiện rất rõ điều này. Một em bé 6 tháng sẽ tuyệt đối không có “ý thức về bản ngã”, nhưng đã có thể có những nhận thức nhất định về thế giới xung quanh. Ý thức hướng nội chỉ tới khi con người trưởng thành hơn. Quá trình trưởng thành về nhận thức của một đời người chính là tấm gương phản chiếu quá trình trưởng thành về nhận thức của toàn thể loài người. Đó chính là lý do để khoa học về nhận thức ra đời quá muộn màng: Trong khi các khoa học khác đã có tới hàng ngàn hoặc hàng trăm năm tuổi, khoa học về nhận thức dường như mới ra đời gần đây. Nói cách khác: Trong khi nền văn minh của nhân loại đã trưởng thành và già dặn qua hàng ngàn năm lịch sử, con người dường như vẫn còn quá ngây thơ trong việc tự hiểu biết mình.

Nhưng hơn bất kỳ một giai đoạn lịch sử nào khác, thế kỷ 20 đã làm cho con người bừng tỉnh: Song song với nhận thức hướng ngoại, con người đã đặc biệt quan tâm tới chính chủ thể nhận thức – nghiên cứu bản chất của nhận thức như nghiên cứu bất kỳ một đối tượng khách quan nào khác!

Nhưng tại sao lại là thế kỷ 20, thay vì thế kỷ 19 hay 21?

Đơn giản vì nhận thức đã phải trả giá rất đắt để hiểu được 3 bài học tưởng như không sao hiểu được trong thế kỷ 20: Thuyết Tương Đối của Einstein + Nguyên Lý Bất Định của Heisenberg + Bài học về cuộc khủng hoảng trầm trọng trong nền tảng Toán Học đầu thế kỷ 20.

Thuyết Tương Đối phải mất vài năm rồi nhân loại mới hiểu.

Nguyên Lý Bất Định cũng phải mất vài chục năm: Ra đời từ 1921 nhưng chưa bao giờ được nhà vật lý lớn nhất thế kỷ 20 là Einstein công nhận, ngay cả trước khi ông mất năm 1955.

Nhưng sự trả giá cho bài học thứ ba còn đắt hơn rất nhiều: Phải mất gần một thế kỷ, tức là đến cuối thế kỷ 20, nhân loại mới bắt đầu hiểu được lý do thực sự của cuộc khủng hoảng Toán Học đầu thế kỷ này. Hơn bất kỳ một bài học nào khác, bài học thứ ba này để lộ giới hạn của nhận thức.

Nếu chọn ngẫu nhiên 100 nhà khoa học và giáo dục để phỏng vấn, có lẽ 100% biết rõ bài học thứ nhất (Thuyết Tương Đối), 75% (hoặc 50%?) biết rõ bài học thứ hai (Nguyên Lý Bất Định), nhưng sẽ có bao nhiêu % biết rõ bài học thứ ba (cuộc khủng hoảng về nhận thức bản chất Toán Học)? Tôi ngờ rằng tỷ lệ này rất thấp, vì thông qua phương pháp giảng dạy môn Toán ở trường phổ thông hiện nay, tôi thấy người ta đã hiểu sai bản chất và ý nghĩa của Toán Học, từ đó suy ra rằng người ta không học được bài học nào từ cuộc khủng hoảng nói trên. Bằng chứng?

Vâng, sẽ có bằng chứng, nhưng xin để dành cho bài viết kỳ sau. Bây giờ là lúc cần quay lại tích “Thầy Bói Xem Voi”, vì chính sự trả giá về nhận thức trong thế kỷ 20 đã làm cho nhân loại bừng tỉnh để “ngộ” ra triết lý sâu xa của truyện ngụ ngôn này: Nhận thức, bản thân nó chứa đựng một NGHỊCH LÝ LỚN – Khát vọng vô hạn về nhận thức mâu thuẫn với bản chất giới hạn của nhận thức!

“Làm thế nào để một bộ phận có thể nhận thức được cái toàn thể?” (How can a part know the whole?), đó chính là nỗi băn khoăn từ thế kỷ 17 của Blaise Pascal – một trong những nhà khoa học và triết học sâu sắc nhất của mọi thời đại.

Một người như Pascal có lẽ có thừa óc tưởng tượng và suy luận để hình dung ra cái tổng thể mà ông khao khát muốn biểt, nhưng dường như cái đầu triết học quá sâu sắc của ông lại khuyên ông nên thận trọng. Phải chăng vì thế mà ông băn khoăn?

Trong thời đại của chúng ta, nỗi băn khoăn của Pascal vẫn mang tính thời sự. Thật vậy, dù khoa học tiến bộ đến mấy, kính viễn vọng có thể nhìn xa đến mấy, kính hiển vi điện tử có thể nhìn sâu đến mấy, cũng chẳng bao giờ nhìn thấy cái tổng thể. Khoa học chỉ suy đoán ra cái tổng thể dựa trên những quan sát bộ phận, rồi lại dùng những quan sát bộ phận để tái kiểm chứng cái mô hình tổng thể đã suy đoán. Dù cho suy đoán dựa trên những phương pháp toán học chính xác bậc nhất, nó vẫn chỉ là kết quả của suy đoán, và do đó nó luôn luôn bị thử thách nghiệt ngã bởi thực tiễn. Thực tiễn luôn luôn là ông thầy chỉ ra lỗi trong các mô hình của con người, buộc con người phải sửa chữa mô hình của mình để phù hợp với hiện thực hơn. Nhưng dù sửa chữa phù hợp đến mấy đi chăng nữa thì cũng chỉ là phù hợp với hiện thực cục bộ có thể quan sát được, thay vì chính cái hiện thực tổng thể tồn tại khách quan, độc lập với mọi suy luận và quan sát của con người.

Chẳng hạn có một thời, Mô Hình Vũ Trụ dựa trên Cơ Học Newton đã thống trị “tuyệt đối” trong tâm thức các nhà khoa học, đến nỗi Joseph Louis Lagrange, nhà toán học lỗi lạc người Pháp trong thế kỷ 18, đã phải thốt lên lời buồn phiền rằng “Newton đã tìm ra hết mọi bí mật rồi, chẳng còn gì lớn cho chúng ta làm nữa”. Nhưng may thay, Albert Einstein đã chứng minh rằng Lagrange sai!

Một số học giả tây phương hiện đại cho rằng nhận thức là một hàm tăng theo thời gian, nhưng không tăng tới vô cùng, mà bị chặn trên bởi một tiệm cận ngang – một cái ngưỡng (threshold): Hàm nhận thức ngày càng tiệm cận tới cái ngưỡng đó nhưng không bao giờ chạm tới và vượt qua!

Thậm chí một số còn cho rằng khoa học ngày nay đã tiến gần đến cái ngưỡng đó. Thời gian sẽ trả lời nhận định này đúng hay sai.

Tuy nhiên, sự tồn tại của một cái ngưỡng là có thật, ít nhất điều này đã được chứng minh trong Toán Học và trong Khoa Học Computer: Đó là “Định Lý Bất Toàn” (Theorem of Incompleteness) của Kurt Godel và “Sự Cố Dừng” (The Halting Problem) của Alan Turing.

Cái ngưỡng đó làm cho một số người nản lòng, thậm chí cảm thấy khó chịu, vì không thể chấp nhận một cái ngưỡng ngáng trở nhận thức. Xin nói ngay rằng những người đó đã hiểu lầm: Chính cái ngưỡng đó làm cho cuộc sống của chúng ta có ý nghĩa hơn, hạnh phúc hơn, và khoa học sẽ đâm chồi nẩy lộc nhiều hơn, đơm hoa kết trái nhiều hơn!

Thật vậy, vì nhận thức có giới hạn, nó không bao giờ đạt tới đích cuối cùng, vì thế khát vọng khám phá sẽ được nuôi dưỡng mãi mãi, niềm vui khám phá sẽ không bao giờ cạn, trí tưởng tượng của con người sẽ tha hồ bay bổng, … điều này làm nên một trong những ý nghĩa căn bản của cuộc sống.

Immanuel Kant vĩ đại từng nói: “Mỗi câu trả lời lại đặt ra một câu hỏi mới”. Bạn nghĩ sao nếu chúng ta tìm ra một câu trả lời cho mọi thứ để rồi không còn gì đáng hỏi nữa? Cuộc sống khi đó sẽ ra sao? Nhưng chính vì không bao giờ có một câu trả lời cuối cùng nên con người tha hồ tưởng tượng để tìm câu trả lời cho những gì mình chưa biết. Nhà toán học kiêm triết học nổi tiếng Bertrand Russell đã an ủi những người lo xa: “Khoa học có thể tạo ra giới hạn đối với sự hiểu biết, nhưng không tạo ra giới hạn đối với trí tưởng tượng”[6].

Nói cách khác, Bà Mẹ Tự Nhiên (The Mother Nature) không bao giờ mở cánh cửa bí mật cuối cùng cho chúng ta, mà luôn để dành những bí mật tiếp theo cho chúng ta khám phá, nhằm nuôi dưỡng chúng ta không chỉ phần xác, mà cả phần hồn!

Bí mật của Tự Nhiên giống như “Chiếc Hộp Trung Hoa” (Chinese Box) hoặc những con búp-bê Matryoshka của Nga – mỗi lần mở ra lại thấy một chiếc hộp bên trong (một con búp-bê bên trong). Mỗi chúng ta đều giống như một đứa trẻ tò mò, trông thấy chiếc hộp bên trong lại muốn mở ra xem, và lại thấy một chiếc hộp bên trong nữa. Albert Einstein chính là một đứa trẻ điển hình như thế, ông nói: “Cái đẹp nhất mà chúng ta có thể chiêm nghiệm chính là sự BÍ ẨN. Đó là ngọn nguồn của nghệ thuật và khoa học chân chính”[7].

Vậy thay vì chống đối nguyên lý giới hạn của nhận thức, chúng ta nên cảm ơn nó, vì nhờ nó chúng ta luôn sống với những khát vọng lãng mạn!

Nhưng cần phải tỉnh táo, vì nếu tham vọng nhận thức trở thành vô chừng vô độ, bất chấp giới hạn thì đó lại là một vấn đề hoàn toàn khác!

Joseph Louis Lagrange
Sinh	25 tháng 1 năm 1736 Torino, Ý
Mất	10 tháng 4 năm 1813 Paris, Pháp
Nơi cư trú	Ý Pháp Phổ
Ngành	Toán học Vật lý học
Nổi tiếng vì	Cơ học giải tích Cơ học thiên thể Giải tích toán học Lý thuyết số

Bertrand Russell

Thời đại	triết học thế kỷ 20
Lĩnh vực	Triết học Phương Tây
Trường phái	Triết học phân tích
Sở thích	Luân lý học, nhận thức luận, logic, toán học, triết học ngôn ngữ, triết học khoa học, tôn giáo
Ý tưởng nổi trội	Thuyết nguyên tử logic, tri thức từ nhận biết và tri thức từ miêu tả, nghịch lý Russell, Ấm chè Russell

3] Khi tham vọng trở nên vô chừng vô độ:

Khi đó, nhận thức có nguy cơ rơi vào không tưởng, lầm đường lạc lối, thay vì tiến lên, nhận thức trở thành một cái vòng luẩn quẩn, hoặc thậm chí thụt lùi.

Lịch sử đã từng chứng kiến phản ứng của những người nhìn xa trông rộng trước những kiểu tham vọng vô chừng vô độ như thế. Một trong những trường hợp đáng để cho chúng ta phải suy ngẫm nghiêm túc lại  là Albert Einstein. Bạn nghĩ sao khi một người như Einstein – một người có khát vọng hiểu biết cháy bỏng hơn ai hết, một đứa trẻ từng say đắm Hình Học Euclid như một kỳ quan, một nhà vật lý cần toán học như chúng ta cần không khí và nước – đã có lúc phải thốt lên:

“Tôi không tin vào Toán Học”[8]!

Thoạt nghe, có vẻ như đó là một chuyện bịa đặt, nhưng than ôi, đó lại là một sự thật! Xin bạn hãy bình tâm tìm hiểu sự thật này, và tôi tin rằng bạn sẽ hết ngạc nhiên nếu biết rõ rằng ấy là lúc Einstein phản ứng với những thứ toán học sáo rỗng, hình thức chủ nghĩa, toán học siêu hình (meta-mathematics), toán học tách rời thực tiễn, toán học thuần tuý suy diễn logic mà không đếm xỉa đến ý nghĩa thực tế.

Bạn sẽ dễ dàng thông cảm với Einstein nếu biết rõ rằng thứ toán học siêu hình đó đã ra đời từ một tham vọng vô chừng vô độ và không tưởng của một số nhà toán học cùng thời với ông. Những người này tin rằng tồn tại những chân lý logic hình thức tuyệt đối, độc lập với thế giới hiện thực xung quanh, và tin rằng với những phương pháp nghiên cứu đúng đắn, trước sau họ cũng sẽ tìm ra những chân lý tuyệt đối đó.

Nhưng Einstein, với trực giác siêu việt, ngay từ đầu đã không tin họ, không tin vào tham vọng ngông cuồng của họ, không tin vào hệ thống toán học thuần lý bất chấp thực tiễn của họ, và lịch sử đã đứng về phía Einstein!

Chẳng riêng Einstein, một vĩ nhân khác mà tài năng chẳng kém gì Einstein là Henri Poincaré, người được coi là Mozart của Toán Học, cũng chống đối quyết liệt thứ toán học sính hình thức đó.

Nhưng than ôi! Sức ỳ của bộ não cũng “vĩ đại” chẳng kém gì sức sáng tạo của nó: Bất chấp những người như Einstein và Poincaré, tư tưởng sính hình thức trong giới toán học, và đặc biệt trong giới giảng dạy toán học, vẫn cứ tiếp tục sống dai dẳng cho đến tận hôm nay.

Nếu đọc giả để ý quan sát, sẽ chẳng mấy khó khăn để nhận thấy bóng dáng những loại toán học này trong hệ thống giáo dục hiện nay. Đó là hậu quả tàn dư của thứ toán học hình thức mà Einstein và Poincaré chán ghét. Đó là lý do để nhiều học giả trên thế giới ngày nay phải lên tiếng cảnh báo: Hãy tỉnh táo để nhận thức nguyên lý giới hạn của nhận thức!

Trong bối cảnh đó, tích “Thầy Bói Xem Voi” tất yếu mang ý nghĩa thời sự và được làm sống lại một cách sinh động dưới nhiều hình thức, điển hình là những “mô hình bất khả” (Impossible Models), hay những “cấu trúc phi lý” (Inconsistent Structures).

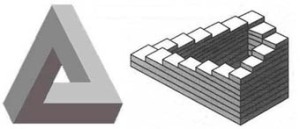
4] Mô Hình Bất Khả:

Điển hình của những mô hình này là Tam Giác Penrose hoặc Bậc Thang Penrose của Sir Roger Penrose, một trong những nhà vật-lý-toán-học lớn nhất ngày nay. Ông có những đóng góp vô cùng đa dạng trong vật lý và toán học, đoạt rất nhiều giải thưởng danh giá bậc nhất về vật lý và toán. Cùng với Stephen Hawking, ông được coi là một trong những tác giả của Lý thuyết về hốc đen, như Wikipedia nhận định: “Công trình sâu sắc của ông về tính Tương Đối Tổng Quát đóng vai trò chủ yếu trong nhận thức của chúng ta về các hốc đen”. Nhưng khác với Stephen Hawking, ông không mấy tin tưởng vào khả năng “Hiểu được ý Chúa” của Einstein trước đây và của Hawking hiện nay. Bản thân những “mô hình bất khả” của ông đã nói lên điều đó.

Ngắm kỹ hai mô hình trên, dễ nhận thấy chúng chỉ “khả dĩ”  (possible) hoặc “hợp lý” (consistent) trong từng cục bộ (local part), nhưng “bất khả” (impossible) hoặc “phi lý” (inconsistent) trên tổng thể (the whole), đúng như triết lý của “Thầy Bói Xem Voi”: Mỗi anh đúng một phần, Nhưng đều sai tất cả!

Tuy nhiên sẽ là bất công nếu gán cho các nhà khoa học công lao sáng tạo ra những “mô hình bất khả”. Chính các hoạ sĩ mới là những người đi tiên phong trong lĩnh vực này. Hãy ngắm bức tranh sau đây:

Đó là cấu trúc “Cầu thang bất khả” (Impossible Staircase) cuả hoạ sĩ Thụy Điển Oscar Reutersvard (1915-2002) được vẽ từ nửa đầu thế kỷ 20! Với hàng trăm mô hình tương tự, Reutersvard được coi là cha đẻ của ngành “hội hoạ ảo ảnh” (Illusionary Art), và chính hội hoạ đó đã tạo cảm hứng cho Penrose sáng tạo ra những mô hình của mình.

Tuy nhiên phải thừa nhận rằng, từ khi những nhà khoa học lớn như Penrose sử dụng các mô hình bất khả để nói lên nguyên lý bất khả trong việc nhận thức CÁI TOÀN BỘ, thì nguyên lý này mới được nhìn nhận một cách thực sự nghiêm túc, không chỉ dưới hình thức văn chương, nghệ thuật, hoặc triết học, mà ngay cả trong lĩnh vực khoa học và công nghệ. Điều này rất có lợi cho cuộc sống, vì nó hướng khoa học vào những công trình thực dụng hơn, thiết thực hơn. Sự chuyển hướng này bộc lộ rất rõ trong những Giải Nobel khoa học từ cuối thế kỷ 20 tới nay (trước đây thường dành cho những đề tài thuần tuý lý thuyết).

Tóm lại, đã có một sự bừng tỉnh về nhận thức đối với triết lý “Thầy Bói Xem Voi”. Để cảm nhận được điều đó, bạn chỉ cần ngồi vào computer rồi gõ “impossible models”, hoặc “artistic illusions”, “inconsistent art”, v.v. bạn sẽ có hàng trăm, hàng nghìn mô hình “bất khả” kỳ lạ khác nhau, trong đó rất nhiều mô hình vừa được công bố chỉ vài ngày trước khi bài báo này đến tay bạn. Điều đó nói lên rằng chủ đề này nóng hổi đến chừng nào.

Tuy nhiên, nếu bạn thật sự muốn biết các nhà khoa học và giáo dục ngày nay nghĩ gì về triết lý “Thầy Bói Xem Voi”, xin bạn hãy đọc ngay một cuốn “best-seller” của năm 1998: “What is Mathematics, Really?” (Thực ra Toán Học là gì?) cuả Reuben Hersh, một nhà toán học rất nổi tiếng ở Mỹ, trong đó tác giả đã dẫn  nguyên văn truyện Sáu anh mù ở xứ Indostan để nói về một “giấc mơ vĩ đại” của các nhà toán học trong thế kỷ 20 – Giấc mơ tìm thấy “Con Voi Toán Học”!

5] Thay lời kết:

Câu chuyện về giấc mơ tìm kiếm Con Voi Toán Học là một trong những chương có ý nghĩa nhất và quan trọng nhất trong lịch sử toán học – quan trọng đến nỗi nếu không biết gì về nó thì không những sẽ vô cùng thiệt thòi vì đã bỏ qua một trong những chương hay nhất, hấp dẫn nhất của lịch sử khoa học, mà còn có nguy cơ bị thiếu hụt một bài học vô giá về khoa học nhận thức và khoa học giáo dục.

Sự thiếu hụt ấy sẽ dẫn tới hậu quả không hiểu rõ bản chất của toán học, và do đó sẽ áp dụng một phương pháp sai lầm trong giảng dạy toán học.Đó chính là điều Reuben Hersh muốn nói, và cũng là điều mà loạt bài viết về chủ đề “Thầy Bói Xem Voi” muốn nói.

Quả thật là đang tồn tại tình trạng hiểu sai bản chất toán học, và đó là lý do căn bản dẫn tới tình trạng “dạy giả” và “học giả” tràn lan: Chưa bao giờ tình trạng học sinh không hiểu Toán, đối phó với Toán, chán Toán, sợ Toán, … ngày càng trở nên phổ biến như hiện nay.

Công bằng mà nói, tình trạng này không chỉ xẩy ra tại Việt Nam, mà đã từng xẩy ra ở ngay tại một số quốc gia  phát triển, khi những quốc gia này áp dụng một phương pháp dạy Toán mà họ tưởng là “mới”. Nhưng lịch sử giáo dục đã chứng minh rằng những phương pháp gọi là “mới” đó thực chất chỉ là sản phẩm của một tham vọng không tưởng – tham vọng tìm kiếm Con Voi Toán Học. Chính vì không tưởng nên nó đã đổ vỡ tan tành!

Tại sao một tham vọng đã đổ vỡ mà vẫn còn ảnh hưởng đến nền giáo dục hôm nay? Đó là một ẩn số cần được trả lời, và sẽ được trả lời trong bài kỳ sau: “Con Voi Toán Học & Chiếc Chén Thánh của Chủ Nghĩa Hình Thức”.

Sydney ngày 01 tháng 01 năm 2009

Phạm Việt Hưng

[1] Nghĩa đen là chiếc chén Chúa Jesus dùng trong bữa tiệc ly với các môn đệ, trước ngày Chúa bị hành hình. Nhưng trong nền văn hoá Tây phương hiện đại, thuật ngữ này thường được dùng với ý bóng, ám chỉ một tham vọng rất lớn lao nhưng không dễ gì đạt được, thậm chí chỉ là một giấc mơ không tưởng và con người không bao giờ với tới.

[2] Dẫn theo cuốn “Impossibility” của John Barrow.

[3] Thí dụ như Reuben Hersh ở Mỹ và Michio Kaku ở Nhật Bản.

[4] Indostan là một tên gọi cổ được sử dụng nhiều trong các thế kỷ 17, 18, 19, để gọi một vùng địa lý mà ngày nay ta gọi là Nam Á, bao gồm Ấn Độ, Pakistan, Bangladesh, Sri Lanka, Maldives, Bhutan và Nepal (những quốc gia nói chung có khí hậu nóng và chịu nhiều ảnh hưởng của nền văn minh Ấn Độ).

[5] Trích bài của La Thiếu Bình, nhan đề “Ý nghĩa sâu xa của truyện Người Mù Sờ Voi”, Khoa Học & Tổ Quốc tháng 08-2009.

[6] Nguyên văn: “Science may set limits to knowledge, but should not set limits to imagination”

[7] Xem “Phương trình của Chúa” của Phạm Việt Hưng trên Khoa Học & Tổ Quốc, số 3+4/2005

[8] Nguyên văn: “I don’t believe in Mathematics”. Xem “Impossibility” của John Barrow.

Nguồn: viethungpham.com

Bài viết đã được chỉnh sửa nội dung bởi LzuTao: 08-07-2015 - 20:36

• NTPS2CBC, 121212 và HungPhuPhan02011964 thích

#2 LzuTao

Sĩ quan
• 
• Thành viên
• 
• 310 Bài viết

• Giới tính:Nam
• Đến từ:$\text{Vũ Trụ}$

Sở thích:$\text{Giúp Người Là Niềm Vui}$

Đã gửi 04-07-2015 - 23:20

ĐỊNH LÝ BẤT TOÀN

Phần 2: "CON VOI TOÁN HỌC" hay "CHIẾC CHÉN THÁNH

CỦA CHỦ NGHĨA HÌNH THỨC"

Bà Mẹ Tự Nhiên (The Mother Nature) đẻ ra không biết bao nhiêu đứa con kỳ lạ, nhưng kỳ lạ nhất vẫn là con người, bởi vì chỉ có con người mới nhận thức được sự tồn tại của chính Bà Mẹ đã đẻ ra nó. Nếu không có con người, Tự Nhiên sẽ trở nên vô nghĩa. Nói cách khác, nhận thức là đặc đặc trưng phân biệt con người với toàn bộ phần còn lại của vũ trụ. Chẳng thế mà Pascal đã định nghĩa “Con người là một cây sậy, một thứ yếu ớt nhất trong tự nhiên, nhưng là một cây sậy có tư tưởng”[1], còn Descartes thì tuyên bố: “Tôi tư duy, vậy tôi tồn tại”[2].

Nhưng dù nhận thức đóng vai trò đặc biệt đến mấy đi chăng nữa, nó vẫn chỉ là một sản phẩm của tự nhiên, và do đó nó phải tuân thủ các định luật của tự nhiên. Một trong các định luật cơ bản của tự nhiên mà nhận thức phải tuân thủ là định luật về giới hạn: Nhận thức không bao giờ đạt tới cái tuyệt đối, cái toàn bộ, cái tận cùng – lý lẽ không thể đi tới cùng kỳ lý! Đó chính là điều John Saxe đã nói ngay từ thế kỷ 19 bằng truyện ngụ ngôn “Thầy Bói Xem Voi”, và đã được Reutersvard hoặc Penrose nhắc lại trong thế kỷ 20 dưới dạng “những mô hình bất khả” (impossible models)[3].

Tuy nhiên, khát vọng nhận thức vốn là một lẽ sống, một hòn than vĩnh cửu cháy âm ỉ trong lòng người, nên nhiều lúc nó bùng lên thành một ngọn lửa lớn, đẩy con người vào những cuộc phiêu lưu đầy tham vọng – tham vọng “biết hết mọi thứ”, “biết đến cùng kỳ lý của sự vật”! Điển hình là cuộc phiêu lưu của Chủ Nghĩa Hình Thức (Formalism) trong toán học đầu thế kỷ 20 hòng khám phá ra “Con Voi Toán Học”, y như chuyện Sáu anh chàng ở xứ Indostanmuốn khám phá ra con voi của họ.

“Con Voi Toán Học” là gì? Xin tạm trả lời vắn tắt: Đó là một hệ thống chân lý tuyệt đối của toán học (tuyệt đối logic, tuyệt đối phi mâu thuẫn)!

Hệ thống chân lý ấy nếu tồn tại, ắt phải rất “thiêng liêng”, rất “vĩ đại”. Nhưng chính toán học đã chứng minh rằng “Con Voi Toán Học” chỉ là một giấc mơ không tưởng, và do đó nó đã được mệnh danh là “Chiếc Chén Thánh[4] của Chủ Nghĩa Hình Thức” (The Holy Grail of Formalism).

Nhưng mặc dù không tưởng, Chủ Nghĩa Hình Thức vẫn như một “bóng ma” ám ảnh mọi nền giáo dục cho đến tận ngày hôm nay.

1] “Bóng ma” của Chủ Nghĩa Hình Thức:

Nếu Chủ Nghĩa Hình Thức chỉ đóng khung trong phạm vi nghiên cứu toán học thì đó là chuyện riêng của các nhà toán học, nhưng vì nó đã xâm nhập vào giáo dục, làm méo mó hệ thống giáo dục, vì thế nó đã trở thành một vấn đề xã hội!

Thật vậy, Chủ Nghĩa Hình Thức vốn coi toán học là một hệ logic hình thức thuần tuý, hoàn toàn tách rời khỏi thế giới hiện thực, nên một khi đã xâm nhập vào giáo dục, nó biến thành một căn bệnh:

Bệnh sính hình thức, sính biến cái đơn giản thành phức tạp, sính sử dụng ký hiệu và ngôn ngữ “hàn lâm” trừu tượng thay cho ngôn ngữ đời sống, đề cao ngôn ngữ này như “tiêu chuẩn” của chân lý, đến nỗi dám coi thường truyền thống giảng dạy của cha ông, tuỳ tiện vứt bỏ hoặc đảo lộn các chương trình kinh điển, rồi chủ quan áp đặt lên trẻ em một chương trình được gọi là “mới” nhưng thực chất chẳng có gì mới, mà chỉ là một sự nhồi nhét hàng đống kiến thức hình thức sáo rỗng, biến môn toán thành một môn học khó hiểu, nặng nề, đẩy học sinh tới chỗ mất kiến thức cơ bản, phải lao đi học thêm lu bù nhằm đối phó với thi cử, miễn sao giành được “miếng cơm manh áo”. Đó chính là tình trạng “dạy giả + học giả” tràn lan hiện nay.

Để chấn chỉnh giáo dục, phải học kỹ lại bài học lịch sử về Chiếc Chén Thánh của Chủ Nghĩa Hình Thức. Học lịch sử chính là học cách nhận thức!

Đó là nhiệm vụ quan trọng bậc nhất của giáo dục mà Henri Poincaré đã từng nhắc nhở chúng ta ngay từ đầu thế kỷ 20: Nhiệm vụ của nhà giáo dục là phải tạo điều kiện để cho nhận thức của trẻ em được trải nghiệm lại tất cả những gì mà tổ tiên của các em đã từng trải qua. Sự trải nghiệm lại phải tiến hành một cách nhanh chóng thông qua những chặng nhất định, nhưng tuyệt nhiên không được lấp liếm bỏ sót một chặng nào cả. Với quan điểm đó, lịch sử khoa học chính là người dẫn đường cho chúng ta[5].

Trong những chặng đường của Chủ Nghĩa Hình Thức, có một chặng rất đặc biệt, không thể lấp liếm bỏ qua, đó là chặng đường của Gottlob Frege, người từng được coi là “Ngọn đèn pha của Chủ Nghĩa Hình Thức”.

2] Ngọn đèn pha của Chủ Nghĩa Hình Thức:

Ngay từ thế kỷ 18, Immanuel Kant đã nói: “Hình học dựa trên trực giác không gian; Số học dựa trên trực giác thời gian”[6].

Bước vào thế kỷ 20, David Hilbert phủ nhận Kant một cách tuyệt đối. Ông cho rằng toán học thực chất là các quan hệ logic, do đó những quan hệ này càng được hình thức hoá cao bao nhiêu thì toán học càng chính xác bấy nhiêu. Nói cách khác, toán học không phải là một khoa học thực dụng như vật lý, hoá học, bởi nó không nghiên cứu bản chất vật chất của các đối tượng, mà chỉ nghiên cứu mối quan hệ logic giữa các đối tượng đó mà thôi. Nếu toán học vấp phải nghịch lý, ấy là vì toán học trước đây vẫn còn vướng quá nhiều “bụi trần”, tức là chưa thật sự toán học, chưa thật sự là một hệ logic thuần tuý hình thức. Muốn có một nền toán học chân chính, phải giải phóng toán học một cách tuyệt đối khỏi thế giới hiện thực, phải hình thức hoá toán học một cách tuyệt đối từ nền móng cho tới thượng tầng. Muốn vậy, phải xây dựng lại toàn bộ cơ sở của toán học, hướng tới mục tiêu cuối cùng là hệ thống “siêu-toán-học” (metamathematics) – một hệ thống logic tuyệt đối siêu hình, hoàn toàn độc lập với thế giới hiện thực, cho phép giải thích và chứng minh mọi mệnh đề toán học cho tới cùng kỳ lý, loại trừ hoàn toàn mọi nghịch lý, mâu thuẫn. Hilbert tin chắc rằng với một phương pháp nghiên cứu đúng đắn, trước sau toán học sẽ đạt tới mục tiêu đó. Câu châm ngôn nổi tiếng của ông, “Chúng ta phải biết, Chúng ta sẽ biết” (Wir müssen wissen, wir werden wissen), được khắc trên bia mộ ông đã nói lên tham vọng “vá trời lấp biển” của ông.

Để chứng minh tư tưởng của mình là đúng và khả thi, bản thân Hilbert đã bỏ công xây dựng lại Hình Học Euclid. Xuất phát từ một hệ 20 tiên đề[7], ông đã xây dựng nên một thứ hình học thuần tuý hình thức, không cần hình vẽ, được gọi là Hình Học Hilbert, ra mắt năm 1899 dưới tên gọi Cơ Sở Hình Học(Grundlagen der Geometrie). Nhưng không thoả mãn với những gì đã làm được, Hilbert kêu gọi toàn thế giới toán học cùng bắt tay vào việc tái thiết toà lâu đài toán học theo “thiết kế” của Chủ Nghĩa Hình Thức.

Mục tiêu tiếp theo là Số Học: Hãy xây dựng cho số học một hệ tiên đề hình thức đầy đủ, độc lập, phi mâu thuẫn, để từ đó xây dựng nên một lý thuyết số học tuyệt đối hình thức. Đó chính là nội dung cơ bản của Bài Toán Số 2 trong số những bài toán ông nêu lên tại Hội Nghị Toán Học Thế Giới ở Paris năm 1900, như một thách thức đối với toán học thế kỷ 20.

Với uy tín lừng lẫy của bản thân, Hilbert đã tập hợp được phần lớn các nhà toán học đương thời dưới ngọn cờ của mình, bao gồm cả một kẻ thù vốn không đội trời chung với ông về hình học, đó là Gottlob Frege.

Thật vậy, Frege đồng ý với Kant rằng hình học dựa trên trực giác, và do đó đã quyết liệt chống đối Hilbert trong ý tưởng biến hình học thành một mớ logic hình thức thuần tuý. Nhưng trớ trêu thay, Frege lại đồng quan điểm với Hilbert khi cho rằng số học dựa trên logic, do đó đã trở thành cứu tinh của Hilbert về mặt số học: Frege đã lao vào làm một cuộc cách mạng về số học, nhằm biến số học thành một hệ logic hình thức thuần tuý, đúng như Hilbert mong muốn!

Để làm cuộc cách mạng đó, Frege bắt đầu xây dựng lại số học từ nền móng – định nghĩa lại khái niệm về số. Với Frege, từ nay số 2 không được hiểu một cách “tầm thường” là 2 con gà, 2 con vịt, … mà phải hiểu là tập hợp của các cặp đôi (pairs); 3 là tập hợp của các “bộ 3” (triples), một cách tổng quát, số là tập hợp của các tập hợp.

Định nghĩa ấy thể hiện tham vọng chính xác hoá các khái niệm toán học đến vô chừng vô độ: Frege đã tìm mọi cách “tẩy rửa”, vứt bỏ mọi ý nghĩa dính dáng đến vật chất cụ thể của số, vì chừng nào số còn gắn với ý nghĩa vật chất cụ thể thì chừng ấy số vẫn chứa đựng bên trong nó những “hạt sạn phi-toán-học” – nguồn gốc dẫn tới nghịch lý mâu thuẫn. Một nhà toán học đã bình luận rằng với  Frege, 3 không phải là “number three” (số 3), mà là “the threeness” (cái 3) (!).

Sau khi thanh tẩy và hình thức hoá tuyệt đối các khái niệm cơ sở của của số học, Frege đã xây dựng nên hàng trăm định lý của số học dưới dạng hình thức tuyệt đối. Toàn bộ lý thuyết của ông đã được công bố trong bộ sách đồ sộ mang tên Cơ Sở Số Học (Grundlagen der Arithmetik), một bộ sách đã làm rung chuyển thế giới toán học. Thật vậy, các nhà toán học theo Chủ Nghĩa Hình Thức đã thật sự bị choáng ngợp trước “vẻ đẹp siêu thoát tinh tuyền hình thức” trong lý thuyết của Frege. Họ phấn chấn đến mức tưởng rằng sắp tìm thấy “Chiếc Chén Thánh”, và tưởng rằng “thiên đường của chủ nghĩa hình thức” đã lấp ló đâu đó ở phía chân trời!

Đó là lúc cuộc đời Frege đạt tới tột đỉnh vinh quang. Tên tuổi của ông nổi lên như sóng cồn. Người ta gọi ông là “ngọn đèn pha của Chủ Nghĩa Hình Thức”. Cuốn Cơ Sở Số Học của ông được tôn vinh như một kiệt tác toán học, sánh vai với những tác phẩm toán học vĩ đại khác, như bộ Cơ Sở của Euclid chẳng hạn, và thậm chí được ca ngợi như cuốn “Kinh Koran của chủ nghĩa logic hình thức”, … (!)

Nếu câu chuyện dừng lại ở đây, thì quả thật không sao nói hết được sự thán phục mà người đời đã dành cho ông, và từ đó cũng có thể hiểu được vì sao Frege đã có một ảnh hưởng sâu đậm và lâu dài trong giới toán học và giáo dục toán học đến như thế: Sâu đậm và lâu dài đến nỗi sau khi lý thuyết của ông sụp đổ, ảnh hưởng của ông vẫn tiếp tục tồn tại – tồn tại không chỉ trong thời của ông và tại quê hương ông, mà tồn tại kéo dài cho tới tận ngày nay trên khắp thế giới, ngay cả trong những nền giáo dục xa lắc xa lơ với ông về mặt không gian lẫn thời gian, trong đó có nền giáo dục Việt Nam.       Ảnh hưởng ấy phổ biến đến nỗi được coi như một thứ chủ nghĩa, được gọi là “chủ nghĩa Frege mới” (Neo-Fregeanism), hoặc chủ-nghĩa-lý-thuyết-logic-tập-hợp(logic-set theoreticism), vì công cụ chủ yếu Frege sử dụng để xây dựng Cơ Sở Số Học là logic và lý thuyết tập hợp.

3] Chủ nghĩa Frege mới:

Cách đây hơn 40 năm, tôi thấy chủ-nghĩa-lý-thuyết-logic-tập-hợp chỉ mới xuất hiện trên trường đại học, mặc dù không nghe thấy vị giáo sư nào nhắc đến cái tên Gottlob Frege. Nhưng hiện nay chủ nghĩa này đã tràn xuống trường phổ thông, mặc dù hầu như không thầy cô giáo dạy toán nào ý thức được rằng mình đang thực hành cái chủ nghĩa do Frege khởi xướng từ một thế kỷ trước đây.

Có lẽ các nhà biên soạn sách giáo khoa và các thầy cô giáo dạy toán của chúng ta hiện nay không ý thức được rằng họ đang hàng ngày sử dụng những ký hiệu và ngôn ngữ của một lý thuyết đã sụp đổ, chẳng hạn ký hiệu ” (mọi), $ (tồn tại), v.v. vì đó chính là những ký hiệu và ngôn ngữ do Frege sáng tác ra khi ông biên soạn bộ Cơ Sở Số Học. Cũng có thể các nhà biên soạn sách giáo khoa và các thầy cô giáo dạy toán của chúng ta càng không ý thức được rằng họ đang bắt chước Frege trong cách trình bầy toán học, sính diễn đạt toán học bằng những ký hiệu trừu tượng hình thức, xa rời ngôn ngữ đời sống, mà hoàn toàn không biết rằng chính Frege cuối cùng đã tự phủ nhận tư tưởng toán học của bản thân mình.

Đó là một sự thật trớ trêu, quá trớ trêu, bởi vì người ta đua nhau bắt chước một phong cách của một tác giả mà chính tác giả ấy đã tự chê bai và từ bỏ. Sự trớ trêu ấy đã làm cho nhà toán học Philip Kitcher phải chua chát thốt lên rằng: “Triết học toán học 30 năm qua chỉ là một chuỗi những ghi chú cho Frege”. Một nhà toán học khác là Reuben Hersh[8], tác giả cuốn “What is Mathematics, Really?” (Thực ra Toán Học là gì?), cũng buồn rầu thừa nhận: “Bất chấp sự thất bại về mặt triết học, chủ nghĩa lý thuyết logic tập hợp vẫn thống trị nền triết học toán học ngày nay”.

Thật vậy, bất chấp những lời trăng trối do chính Frege để lại, hậu thế vẫn tiếp tục đi theo vết xe đổ của ông. Đó là một hiện tượng kỳ quái, khó hiểu, và có thể là độc nhất vô nhị trong lịch sử khoa học nói chung và toán học nói riêng. Để “giải mã” hiện tượng kỳ quái đó, có người vội đặt dấu hỏi nghi vấn: Phải chăng trong di sản của Frege vẫn có cái hay cái đẹp đáng bắt chước, vì thế mới có “chủ nghĩa Frege mới”?

Xin trả lời ngay rằng KHÔNG!

Những ai còn nghĩ như thế thì chỉ chứng tỏ rằng người đó không biết gì về Frege, không biết gì về những lời trăng trối của Frege, không biết gì về lịch sử toán học thế kỷ 20, không biết gì về những bài học đã được rút ra từ lịch sử đó. Những người này có thể từng được coi là “giỏi toán”, có một vốn liếng toán học tiếp thu từ những thập kỷ cách đây vài chục năm, nhưng sau đó chỉ đem những vốn liếng đó ra hành nghề giảng dạy mà không chịu tiếp tục học hỏi mở mang thêm, không biết rằng thế giới đã thay đổi, đặc biệt từ cuối thế kỷ 20 cho đến nay, do đó vẫn tiếp tục “nằm trong chăn” để tụng niệm ngôn ngữ của Frege, coi đó là ngôn ngữ chân chính và duy nhất của toán học, và do đó vô tình tiếp tục nuôi dưỡng Chủ Nghĩa Hình Thức.

Với những người mê ngủ đó, cần phải gõ lên tiếng kẻng báo động: Chủ Nghĩa Hình Thức đã lỗi thời rồi, thậm chí đã chết rồi, chỉ còn cái “bóng ma” của nó vẫn cứ ám ảnh những nhà giáo dục mê ngủ mà thôi!

Thật vậy, cả Hilbert lẫn Frege đều đã bị chứng minh là nhầm lẫn. Định Lý Bất Toàn (Theorem of Incompleteness) của Kurt Gödel đã phủ nhận toàn bộ chương trình Hilbert, phủ nhận toàn bộ công trình hình thức hoá số học của Frege.

Kết luận trên có thể làm cho một số “học giả” dẫy nẩy lên phản ứng: Phủ nhận hình thức hoá là phủ nhận toán học, vì hình thức hoá là một phương tiện không thể thiếu của toán học, nhờ hình hức hoá mới có toán học ngày nay, chẳng hạn, nếu không hình thức hoá thì làm gì có số ảo i = , làm gì có lý thuyết số phức, làm gì có khoa học logic, và do đó làm gì có khoa học computer ngày nay, v.v. Vậy phủ nhận hình thức hoá tức là chống lại toán học, chống lại khoa học (!).

Với những “học giả” đó, cần phải nhắc lại điệp khúc “biết rồi, khổ lắm, nói mãi”, và đặc biệt, phải trích ý kiến của Reuben Hersh trong cuốn “Thực ra Toán Học là gì?” (đã dẫn). Hersh viết:

Logic là gì?          Phải chăng đó là những quy luật tư duy chính xác? Kinh nghiệm thường ngày và những nghiên cứu phong phú của các nhà tâm lý học cho thấy phần lớn tư duy của chúng ta không tuân theo logic. Từ đó suy ra rằng, hoặc phần lớn tư duy của con người là sai, hoặc logic chỉ tác động trong một phạm vi quá hẹp. Computers chính là những chiếc máy tuân thủ logic, đó chính là câu trả lời! Logic là những quy tắc của máy tính! Logic cũng áp dụng cho con người khi con người cố gắng biến mình thành những chiếc máy tính!

Xin nói rõ thêm: Bài viết này không phản đối nhu cầu hình thức hoá trong nghiên cứu toán học, nhưng phản đối việc hình thức hoá, máy móc hoá, chương trình hoá bộ não của học sinh! Học sinh là con người chứ không phải những chiếc máy tính, đúng như Hersh đã nói! Xin đừng cố gắng biến học sinh thành máy tính! Xin các nhà giáo dục hiểu cho rằng đối tượng của giáo dục là con người chứ không phải những chiếc máy! Nghệ thuật của sư phạm có những đặc điểm riêng mà một người “giỏi toán” có thể không hiểu, bởi vì bản chất của giáo dục là KHAI TÂM chứ không phải là nhồi nhét kiến thức! Ngay cả đối với sinh viên đại học chứ đừng nói tới học sinh, việc khai tâm vẫn quan trọng hơn khai trí, bởi vì một khi tâm đã động thì học sinh và sinh viên có thể tự học, tự nghiên cứu, tự mở mang, và sẽ trở thành một trí thức chân chính, trong khi những con vẹt được điểm 10 trong thi cử sẽ chỉ trở thành những chiếc máy tính loại xoàng. Rất tiếc là lối dạy học nhồi nhét hình thức ngày nay chủ yếu chỉ tạo ra những con vẹt nhiều hơn là những trí thức chân chính!

4] Thay lời kết:

Riêng Frege, không cần đợi đến khi Định Lý Bất Toàn ra đời, ông đã thay đổi quan điểm, tự ông đã phê phán tính hão huyền của Chủ Nghĩa Hình Thức. Tại sao bỗng nhiên Frege thay đổi, và Frege đã thay đổi như thế nào? Đó là một bí mật lý thú cần phải làm sáng tỏ, và sẽ được làm sáng tỏ.

Rất tiếc là nhiều nhà giáo dục hiện nay đang bắt chước Frege lại không hề biết điều đó, và do đó họ không ý thức được rằng việc ra sức nhồi nhét vào đầu trẻ em những khái niệm trừu tượng xa rời thực tiễn không những chứng tỏ sự thiếu hiểu biết về lịch sử toán học, đồng thời còn tỏ ra thiếu hiểu biết về nghệ thuật sư phạm.

Sydney ngày 12 tháng 02 năm 2009

Phạm Việt Hưng

[1] L’homme est un roseau, le plus faible de la nature, mais c’est un roseaupensant.

[2] Je pense, donc je suis.

[3] Xem “Thầy Bói Xem Voi” (Phần 1) của Phạm Việt Hưng, Khoa Học & Tổ Quốc số Tháng 02-2009.

[4] “Chiếc Chén Thánh” (The Holy Grail) là một thuật ngữ  có nghĩa đen là chiếc ly Chúa Jesus đã dùng trong bữa tiệc cuối cùng với các môn đệ trước khi Chúa bị hành hình. Nhưng thuật ngữ này thường được dùng trong nền văn hoá tây phương với nghĩa bóng, ám chỉ những khát vọng có thể rất thiêng liêng, vĩ đại, nhưng quá xa vời, rất khó với tới, thậm chí không bao giờ với tới.

[5] Trích “L’enseignement mathématique”, Henri Poincaré, 1899

[6] Xem “What is Mathematics, Really?”, Reuben Hersh, Chapter 7, Immanuel Kant

[7] Xem thêm: “Hệ tiên đề Hilbert có hoàn hảo?”, Phạm Việt Hưng, Tia Sáng tháng 08-2002.

[8] Giáo sư danh dự Đại học New Mexico, nổi tiếng vì những công trình triết học toán học, từng đoạt Giải Thưởng Sách Quốc Gia Mỹ năm 1983 nhờ cuốn “Mathematical Experience”. Cuốn “What is Mathematics, Really?” được đánh giá là một “outstanding book” (một cuốn sách nổi bật) của năm 1998.

Nguồn: viethungpham.com

Bài viết đã được chỉnh sửa nội dung bởi LzuTao: 05-07-2015 - 15:07

• hxthanh và 121212 thích

#3 LzuTao

Sĩ quan
• 
• Thành viên
• 
• 310 Bài viết

• Giới tính:Nam
• Đến từ:$\text{Vũ Trụ}$

Sở thích:$\text{Giúp Người Là Niềm Vui}$

Đã gửi 04-07-2015 - 23:38

ĐỊNH LÝ BẤT TOÀN

Phần 3: LỜI SÁM HỐI của một nhà toán học

hình thức

Gottlob Frege: “Nghịch lý tập hợp đã huỷ hoại lý thuyết tập hợp”

Nếu lòng dũng cảm và tính trung thực là thước đo nhân cách của một nhà khoa học thì Gottlob Frege (1848-1925) phải được coi là một trong những nhà khoa học có nhân cách vĩ đại nhất: Mặc dù cay đắng đến tột cùng khi tác phẩm để đời của ông – cuốn Cơ Sở Số Học(1) – bị sụp đổ tan tành chỉ vì một nghịch lý đã được phát hiện ngay trong nền tảng lý thuyết, nhưng Frege không tìm cách né tránh hoặc ngụy biện, mà ngược lại, đã xử sự như một người quân tử: Công khai thừa nhận sai lầm và rứt khoát từ bỏ lý tưởng toán học hình thức mà ông đã ấp ủ cả cuộc đời. Một năm trước khi mất, ông để lại những lời trăng trối vô cùng cảm động, như một lời sám hối về nhận thức sai lầm đối với bản chất của toán học.

“Lời của kẻ sắp mất là lời khôn”: Năm 1931, Kurt Godel công bố Định Lý Bất Toàn (Theorem of Incompleteness), cho thấy lý tưởng của Chủ Nghĩa Hình Thức chỉ là một ảo tưởng hão huyền – một cái vòng luẩn quẩn của kẻ đi tìm điểm cuối trên một đường tròn!

Trớ trêu thay, người vạch ra sai lầm của Frege lại là người vốn ngưỡng mộ Frege hết lòng: Đó là Bertrand Russell (1872-1970), một người luôn luôn khao khát tìm kiếm chân lý tuyệt đối của toán học như một con chiên ngoan đạo khao khát đức tin tôn giáo.

1] “Tôn giáo” của Bertrand Russell:

Trong cuốn “Portraits from Memory” (Những chân dung qua trí nhớ) Russell viết: “Tôi khao khát tìm kiếm cái chắc chắn (certainty) giống như người ta khao khát đức tin tôn giáo. Tôi nghĩ tính chắc chắn dường như có trong toán học nhiều hơn ở bất kỳ nơi nào khác”(2). Nhưng ông không thoả mãn với những thứ toán học mà ông đã biết: “Tôi khám phá ra rằng nhiều chứng minh toán học, mà các thầy giáo của tôi muốn tôi chấp nhận, chứa đựng đầy rẫy sai lầm”(3), Russell viết. Vì thế, ông cho rằng cần phải xây dựng lại toán học, sao cho toán học trở thành một hệ thống chân lý thật sự đáng tin cậy: “Nếu tính chắc chắn thật sự có thể tìm thấy trong toán học thì đó sẽ là một lĩnh vực mới của toán học, với những nền tảng vững chắc hơn những nền tảng mà cho tới nay người ta tưởng là đã vững chắc lắm rồi”(4).

Với tư tưởng đó, Russell đã nghiễm nhiên gia nhập “phái nền tảng” (foundationism) – trường phái đòi xét lại nền tảng của toán học đầu thế kỷ 20. Phái này cũng chính là “phái hình thức” (formalism), bởi họ cho rằng muốn xây dựng lại toán học, phải triệt để hình thức hoá toàn bộ toán học, biến toán học thành một hệ logic tuyệt đối siêu hình, hoàn toàn tách rời thế giới hiện thực, như Russell tuyên bố: “Toán học là một khoa học mà trong đó người ta không bao giờ biết người ta đang nói về cái gì, miễn là cái điều người ta nói là đúng”(5). Chẳng hạn, khi xét mệnh đề  2 + 3 = 5, toán học “chân chính” không cần biết ý nghĩa vật chất cụ thể của các số 2, 3, 5 là cái gì, miễn là có được những định nghĩa và tiên đề nào đó về số cho phép kiểm tra mệnh đề đã cho là đúng hay sai. Nói cách khác, Russell coi bản chất toán học là logic, toán học đồng nghĩa với logic-học: Đó chính là chủ nghĩa logic (logicism) mà Frege đã áp dụng để xây dựng bộ Cơ Sở Số Học và David Hilbert cũng đã áp dựng trước đó để xây dựng cuốn Cơ Sở Hình Học(6).

Chủ nghĩa ấy giống như một thứ “tôn giáo thiêng liêng”: “Tôi tin rằng toán học là nguồn chủ yếu của niềm tin vào chân lý vĩnh cửu và chính xác, cũng như vào một thế giới siêu việt có thể nhận biết được bằng trí óc”(7), Russell viết. Chính vì khao khát nhận biết được cái “thế giới siêu việt” ấy nên Russell đã bàng hoàng xúc động khi đọc Cơ Sở Số Học của Frege, coi Frege như một ngôi sao dẫn đường của toán học hình thức.

Nhưng ngưỡng mộ Frege bao nhiêu, ông cũng lo lắng cho Frege bấy nhiêu, vì ông cảm thấy một nghịch lý do chính ông khám phá ra trước đó có thể huỷ hoại công trình của Frege. Đó là “Nghịch Lý Russell” (Russell’s Paradoxe), một nghịch lý đã đi vào lịch sử toán học như một trong những nghịch lý nổi tiếng nhất!

2] Nghịch lý Russell:

Russell chia tập hợp thành hai loại:

1* Tập thông thường (ordinary set), là tập hợp sao cho nó không phải là phần tử của chính nó (nó không thuộc chính nó). Thí dụ: Tập hợp những chiếc xe máy là một tập thông thường, vì tập hợp ấy không thể là một chiếc xe máy.

2* Tập lạ thường (extraordinary set), là tập hợp sao cho nó là phần tử của chính nó (nó thuộc chính nó). Thí dụ: Tập hợp của tất cả những gì không phải là chiếc xe máy. Dễ thấy tập hợp này là một phần tử của chính nó, vì tập hợp này không phải là một chiếc xe máy.

Có rất nhiều tập thông thường khác nhau cũng như có rất nhiều tập lạ thường khác nhau. Russell đề nghị xét một tập hợp đặc biệt, đó là Tập hợp của tất cả các tập thông thường. Ngay lập tức, cái đầu logic sắc sảo của Russell dẫn ông tới một câu hỏi lạ lùng nhưng lý thú:

Tập hợp của tất cả các tập thông thường là một tập thông thường hay lạ thường?

Câu hỏi trên dài quá, có thể làm mệt một số độc giả. Vậy xin rút gọn bằng cách gọi tập hợp của tất cả các tập thông thường là Tập Russell.

Khi đó, câu hỏi của Russell sẽ là:

Tập Russell là một tập thông thường hay lạ thường?

Giả sử Tập Russell là tập thông thường, lập tức suy ra nó là một phần tử của chính nó (vì Tập Russell chứa tất cả các tập thông thường). Nhưng nếu nó là một phần tử của chính nó thì nó phải là tập lạ thường, vậy Tập Russell là tập lạ thường, mâu thuẫn với giả thiết!

Giả sử ngược lại cũng dẫn tới mâu thuẫn. Tóm lại:

· Nếu Tập Russell là tập thông thường thì nó sẽ là tập lạ thường.

· Nếu Tập Russell là tập lạ thường thì nó sẽ là tập thông thường.

Đó chính là Nghịch lý Russell, được trình bầy dưới dạng ký hiệu như trong minh hoạ sau:

Hình bên trái: Một cái hộp chứa chính nó - một sản phẩm phi thực tế. Hình bên phải: Một tập hợp chứa chính nó - một sản phẩm của logic hình thức thuần tuý.

Logic hình thức thừa nhận một khái niệm phi hiện thực – nguồn gốc của mâu thuẫn nghịch lý

“Thủ phạm” dẫn tới nghịch lý là Tập Russell, tức tập hợp của tất cả các tập thông thường. Đó cũng chính là “thủ phạm” gây ra BẤT ỔN ngay từ trong nền móng lý thuyết của Frege, bởi Frege đã xây dựng toà lâu đài số học của mình dựa trên khái niệm nền tảng là “tập hợp của các tập hợp”: 2 là tập hợp của các cặp đôi; 3 là tập hợp của các “bộ ba”, …

Vốn ngưỡng mộ Frege hết lòng, Russell vội tìm cách cứu Frege. Ông viết thư thông báo cho Frege biết nghịch lý của mình, hy vọng Frege có thể sửa chữa được công trình, nhưng không ngờ lá thư ấy đã đẩy Frege xuống vực thẳm thất vọng, để cuối cùng dẫn ông tới một cuộc sám hối sâu sắc về nhận thức bản chất của toán học.

3] Lá thư quyết định số phận của Frege:

Ngày 16-06-1902, Bertrand Russell gửi tới Frege một lá thư, trong đó có đoạn viết: “Trong công trình của ngài, tôi tìm thấy những lý thuyết đẹp đẽ nhất trong thời đại của chúng ta mà tôi biết, và do đó tôi tự cho phép mình bầy tỏ một sự kính trọng sâu xa đối với ngài”(8).

Russell không chỉ viết thư cho cá nhân Frege, mà còn giới thiệu công trình của Frege với toàn thế giới, mà trước đó hầu như nó không được ai biết đến. Có lẽ tính hình thức quá nặng nề làm cho nó trở nên khô khan, khó hiểu, không hấp dẫn. Nhưng Russell “tiêu hoá” được nó, ngưỡng mộ nó, vì chính ông cũng đang cùng với Alfred Whitehead viết một công trình tương tự: Principia Matematica (Nguyên Lý Toán Học). Nhưng tại sao Russell đã khám phá ra nghịch lý của ông từ một năm trước khi gửi thư tới Frege, mà trong thư ông vẫn coi công trình của Frege là một đột phá, một lý thuyết đẹp đẽ nhất? Đơn giản vì Russell không bao giờ từ bỏ khát vọng tìm kiếm một hệ thống chân lý tuyệt đối của toán học. Có thể ông cho rằng về căn bản Frege đã đi đúng hướng, vấn đề là Frege chỉ cần xem xét lại, sửa chữa công trình sao cho hoàn chỉnh hơn mà thôi!

Hoá ra tác giả của một trong những nghịch lý nổi tiếng nhất của toán học cũng không ý thức được rằng bản chất của toán học cũng như mọi hệ thống nhận thức khác vốn bất toàn – không tồn tại một hệ logic tuyệt đối phi mâu thuẫn – như 29 năm sau đó Godel đã chứng minh.

Đó là lý do để Russell thông báo cho Frege biết nghịch lý của mình với một thái độ rất tao nhã, khiêm tốn: “Tôi tán thành với ngài về mọi điểm, nhưng chỉ có một điểm tôi gặp phải khó khăn …”(9).

Nhưng trong khi Russell khiêm tốn như thế thì chính Frege lại nhanh chóng nhận thấy nguy cơ sụp đổ toàn bộ công trình của đời mình.

Với bản chất trung thực, thẳng thắn hiếm có, ông lập tức viết thư trả lời Russell, và viết ngay một phụ lục bổ xung vào Tập 2 của bộ Cơ Sở Số Học đúng vào lúc nó chuẩn bị được đem in, như một sự công khai thừa nhận thất bại của mình: “Không còn gì tồi tệ hơn có thể xẩy đến với một nhà khoa học khi phải chứng kiến nền tảng lý thuyết của mình sụp đổ đúng vào lúc công trình được hoàn thành. Tôi đã bị đặt vào tình thế này do vừa nhận được một lá thư từ ngài Bertrand Russell”(10).

Nhà khoa học có thể gặp nhiều nỗi cay đắng, nhưng hiếm có nỗi cay đắng nào giống như của Frege: Ông mất năm 1925 với tâm trạng của một kẻ tin rằng công trình của cả cuộc đời mình chỉ dẫn tới sự vô ích. Cái chết của ông không được cộng đồng khoa học biết tới(11).

Thật là đau đớn, chua chát, nhưng có lẽ nỗi chua chát lớn nhất đối với Frege là sự vô tình của người đời trước những lời trăng trối vô cùng tha thiết của ông – những lời sám hối mà lẽ ra mọi người phải biết rõ.

4] Những lời sám hối của Frege:

Năm 1924, tức một năm trước khi mất, Frege trăng trối: “Nghịch lý tập hợp đã huỷ hoại lý thuyết tập hợp”. Rồi ông nói tiếp: “Tôi càng suy nghĩ về điều này thì tôi càng đi đến chỗ tin rằng số học và hình học đều nẩy sinh từ cùng một nền tảng, thực ra là từ nền tảng hình học; Do đó toàn bộ toán học thực ra là hình học”(12).

Nghĩa là ông đã vĩnh biệt giấc mơ hão huyền của chủ nghĩa hình thức để trở về với cái nôi hiện thực – cái nôi đã đẻ ra toán học. Để thấu hiểu cuộc “lột xác” này, xin độc giả nhớ lại quan điểm của Frege về hình học:

Về hình học, ngay từ đầu Frege đã là một môn đệ trung thành của trường phái Kant, coi hình học là khoa học dựa trên trực giác, tức là dựa trên thực tiễn, và do đó đối kháng 100% với David Hilbert khi Hilbert muốn biến hình học thành một hệ logic hình thức thuần tuý.

Hilbert vốn đã nổi tiếng nhưng lại càng nổi tiếng hơn vì một tuyên bố “bất hủ” của ông: “Bất kể lúc nào người ta cũng có thể nói về điểm, đường, mặt như là nói về cái bàn, cái ghế, và cốc bia”(13). Có nghĩa điểm, đường, mặt trong thực tế là cái gì cũng không quan trọng, điều quan trọng là chúng có thoả mãn các mệnh đề logic (tiên đề, định lý) của hình học hay không.

Ngược lại, đối với Frege, ý nghĩa của một mệnh đề hình học gắn chặt với ý nghĩa của những đối tượng hình học nằm trong mệnh đề đó. Nếu không hiểu hoặc hiểu sai những đối tượng này thì mệnh đề hình học cũng bị hiểu sai hoặc trở nên vô nghĩa. Ông viết: “Chừng nào mà tôi hiểu những từ như “đường thẳng”, “song song”, “giao điểm” như tôi vẫn hiểu, thì chừng ấy tôi không thể không chấp nhận tiên đề đường song song. Nếu ai đó không chấp nhận nó, tôi chỉ có thể cho rằng người ấy hiểu những từ ngữ này không giống tôi. Ý nghĩa của những từ ngữ đó gắn chặt với tiên đề đường song song”(14). Điều đó có nghĩa là Hilbert hoàn toàn sai khi không đếm xỉa đến ý nghĩa thực tế của các đối tượng hình học như điểm, đường, mặt.

Trong thực tế, mâu thuẫn quan điểm hình học giữa Frege và Hilbert đã bùng nổ thành một cuộc tranh cãi không thể thoả hiệp, như Reuben Hersh đã kể lại như sau:

Quan điểm theo trường phái Kant của Frege về hình học đã dẫn ông tới chỗ tấn công Hilbert. Ông nói với Hilbert rằng Hilbert không biết phân biệt một định nghĩa với một tiên đề. Hilbert đã trả lời thư đầu tiên của Frege hoặc hai thư. Sau đó Hilbert lờ đi. Nhưng Frege tiếp tục lớn tiếng. Thậm chí ông nói xa nói gần rằng Hilbert không dám tiếp tục tranh cãi nữa vì sợ những kết quả của mình có thể sai!(15)

5] Kết:

Henri Poincaré, một trong những nhà toán học vĩ đại nhất của mọi thời đại, ngay từ đầu đã quyết liệt chống đối chủ nghĩa logic hình thức. Khi Nghịch Lý Russell ra đời, ông không cần che giấu sự thoả mãn khi công khai bình luận ý nghĩa tích cực của nghịch lý này với một giọng đầy giễu cợt đối với chủ nghĩa logic hình thức: “Chủ nghĩa logic cuối cùng cũng đã chứng minh được rằng nó không hoàn toàn vô ích. Phút chót nó cũng đã sinh đẻ được, nhưng lại đẻ ra một nghịch lý”(16).

Có lẽ Frege cũng nghĩ như vậy nên mới đi đến chỗ sám hối và “lột xác” 100% trong những năm cuối đời. Sự sám hối của ông là bài học vô giá, giúp chúng ta nhận ra rằng:

· Nghịch lý Russell đã huỷ hoại lý thuyết tập hợp. Nếu nó chưa đủ sức khai tử Chương Trình Hilbert như 29 năm sau Định Lý Bất Toàn của Godel sẽ làm, thì ít nhất nó cũng đã cho thấy lý thuyết tập hợp thực ra cũng chẳng phải “lý tưởng”, “chính xác”, và “tuyệt đối” như người ta đã kỳ vọng quá nhiều vào nó – kỳ vọng đến nỗi coi nó là nền tảng của toán học, muốn dùng nó làm cơ sở để diễn đạt toàn bộ toán học, và thậm chí, ra sức nhồi nhét ngôn ngữ tập hợp vào đầu học sinh phổ thông.

Thiết tưởng lời giễu cợt của Poincaré nói trên và sự sám hối của Frege cũng đã quá đủ để cho những ai có những kỳ vọng đó phải hồi tâm suy nghĩ lại. Nếu uy tín của Poincaré và Frege chưa đủ để “lay chuyển” sức ỳ của những bộ não sính hình thức chủ nghĩa thì xin cung cấp thêm một nhận định của Bách Khoa Toàn Thư Triết Học Stanford (Stanford Encyclopedia of Phylosophy) của Đại Học Stanford ở Mỹ như sau:

Ý nghĩa của Nghịch Lý Russell có thể cảm nhận được rõ ràng một khi hiểu ra rằng dựa trên logic cổ điển, mọi mệnh đề đều dẫn tới mâu thuẫn. Do đó trong con mắt của nhiều người, dường như không có một chứng minh toán học nào đáng tin cậy, một khi logic và lý thuyết tập hợp vốn là nền tảng của toán học lại là mâu thuẫn(17).

Điều này có nghĩa là gì? Có nghĩa là toán học cũng chỉ chính xác đến một mức độ tương đối nào đó mà thôi, thay vì có thể đạt tới sự chính xác tuyệt đối như nhiều người vẫn tưởng. Sự đề cao thái quá ngôn ngữ logic và tập hợp như “cây đũa thần” của toán học chỉ để lộ ra sự thiếu hiểu biết về bản chất của toán học! Nếu bài học của Frege vẫn chưa đủ để nhắc nhở những người mắc bệnh sính hình thức trong giáo dục cần xem xét lại phương pháp giảng dạy của mình thì có lẽ nên nói thêm về Định Lý Bất Toàn của Kurt Godel, Sự Cố Dừng của Alan Turing, Số Omega của Gregory Chaitin. Nhưng xin dành những chuyện đó cho bài kỳ sau.

Sydney ngày 21 tháng 04 năm 2009

Phạm Việt Hưng

Ghi Chú:

(1) “Die Grundlagen der Arithmetik”, Gottlob Frege, Tập I ra mắt năm 1884, Tập II ra mắt vào năm 1902, ngay sau khi Frege được biết Nghịch Lý Russell.

(2) (3) (4) (7) “What is Mathematics, Really?”, Reuben Hersh, Vintage, London, 1998, Trang 151.

(5) “Pour la SCIENCE, Les Génies de la Science, Henri Poincaré, Phylosophe et Mathématicien”, T.21

(6) “Die Grundlagen der Geometrie”, David Hilbert, xuất bản lần đầu năm 1899, tái bản và sửa chữa rất nhiều lần. Để hiểu thêm tài liệu này, xin đọc thêm “Hệ tiên đề Hilbert có hoàn hảo?” của Phạm Việt Hưng, Tia Sáng Tháng 08-2002.

(8) (9) (10) “Engines of Logic, Mathematicians & the Origin of the Computer”, Martin Davis, WW Norton & Company, New York, London 2000, T.41

(11) Tài liệu ghi chú (8) T.43

(12) (15) Tài liệu ghi chú (2) T.150

(13) (14) “Frege and Hilbert on the Foundations of Geometry”, Susan G. Sterrett

(16) Tài liệu ghi chú (2) T.200

(17) Stanford Encyclopedia of Philosophy, Russell’s Paradoxe

http://stanford.libr...ussell-paradox/

Nguồn: viethungpham.com