CÁC BẬC NHÂN TÀI KHOA HỌC 15
(ĐC sưu tầm trên NET)
43-Pierre de Fermat

1601-1665
Pháp
Toán Học
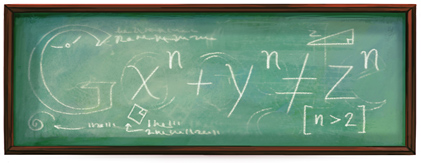



Câu chuyện về định lý cuối cùng của Fermat là câu chuyện độc nhất vô nhị trong lịch sử toán học thế giới, khởi nguồn từ cổ đại với nhà toán học Pythagore. Bài toán cuối cùng của Fermat (sau này giới toán học gọi là Định lý cuối cùng của Fermat, hay Định lý lớn Fermat) có gốc từ định lý Pythagore: “Trong tam giác vuông thì bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông”. Và Fermat thay đổi phương trình Pythagore sau đó tạo ra một bài toán "siêu khó" đến mức bất hủ.
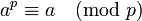
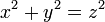
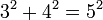
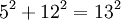
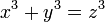

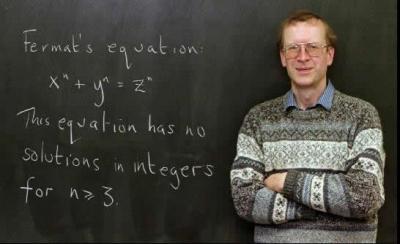 Đây chính là giáo sư Andrew Wiles "siêu nhân" đã chứng minh được định lý lớn Fermat
Đây chính là giáo sư Andrew Wiles "siêu nhân" đã chứng minh được định lý lớn Fermat
Pierre de Fermat sinh ngày 17/8/1601 tại Beaumont-de-Lomagne, Pháp trong một gia đình khá giả. Ông học ở Toulouse về luật dân sự, sau đó làm chánh án. Tuy vậy, Fermat lại vô cùng say mê toán học với thói quen nổi tiếng là ghi các ghi chú bên lề các quyển sách.
Nhà nghiên cứu lịch sử toán học nổi tiếng E.T.Bell đã từng gọi Fermat là "Hoàng tử của những người nghiệp dư". Bell cho rằng Fermat đã đạt được nhiều thành tựu toán học quan trọng hơn hầu hết các nhà toán học "chuyên nghiệp" cùng thời với ông.
Fermat rất say mê các công trình toán học của người Hy Lạp cổ đại, chính các công trình như Archimedes và Eudoxus đã gợi ý cho Fermat xây dựng khái niệm các phép toán giải tích.
Ông cố gắng tổng quát hóa các công trình toán học cổ điển và tìm ra nét mới trong kho tàng các phát minh đã bị chôn vùi từ rất lâu, như ông đã từng nói: "Tôi đã tìm được rất nhiều định lý đẹp vô cùng".
Mãi sau khi Fermat mất (12/1/1665), con trai ông mới in dần các công trình của cha kể từ năm 1670. Đến năm 1896, hầu hết các tác phẩm của Fermat được ấn hành thành 4 tập dày. Người ta đã vô cùng ngạc nhiên và khâm phục trước sự đóng góp lớn lao của ông.
Trong hình học, Fermat phát triển ra phương pháp tọa độ, lập phương trình đường thẳng và các đường cong bậc hai rồi chứng minh rằng các đường cong nọ chính là các thiết diện cônic. Trong toán giải tích, ông nêu các quy tắc lấy đạo hàm của hàm mũ với số mũ bất kỳ, tìm cực trị, tính tích phân những hàm mũ với số mũ phân số và số mũ âm.
Trong vật lý, chúng ta quá quen thuộc nguyên lý Fermat về truyền sáng, đó là một định luật quan trọng của quang học.
Nhưng đóng góp quan trọng nhất trong toán học của Fermat là lý thuyết số hiện đại, trong đó có 2 định lý nổi bật: định lý nhỏ Fermat và định lý lớn Fermat (định lý cuối cùng của Fermat).
Câu chuyện về định lý cuối cùng của Fermat là câu chuyện độc nhất vô nhị trong lịch sử toán học thế giới, khởi nguồn từ cổ đại với nhà toán học Pythagore.
Bài toán cuối cùng (sau này giới toán học gọi là Định lý cuối cùng của Fermat, hay Định lý lớn Fermat) có gốc từ định lý Pythagore: "Trong một tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông". Fermat thay đổi phương trình Pythagore và tạo ra một bài toán khó bất hủ.
Xét phương trình Pythagore: x2 + y2 = z2
Người ta có thể hỏi những nghiệm số nguyên của phương trình này là gì, và có thể thấy rằng: Có vô số nghiệm nguyên chẳng hạn (3,4,5) và (5,12,13).
Fermat khi đó xét dạng bậc ba của phương trình này: x3 + y3 = z3.
Đối với câu hỏi có thể tìm được nghiệm (nguyên) cho phương trình bậc ba này hay không? Fermat đã khẳng định là không. Thực ra, ông khẳng định điều đó cho họ phương trình tổng quát : xn + yn = zn với n là số nguyên lớn hơn 2. Đó là Định lý Fermat cuối cùng.
Gắn liền với định lý này là câu chuyện rất hay, đó là Fermat cho rằng không thể tìm được nghiệm (nguyên) cho phương trình bậc ba. Điều lý thú ở đây là phỏng đoán này được Fermat ghi bên lề một cuốn sách mà không chứng minh, nhưng có kèm theo dòng chữ: “Tôi có một phương pháp rất hay để chứng minh cho trường hợp tổng quát, nhưng không thể viết ra đây vì lề sách quá hẹp.”
Với những dòng viết tay đó, nhà toán học người Pháp Pierre de Fermat đã chính thức buông lời thách đố đối với thế hệ các nhà toán học sau ông. Nhiều nhà toán học đã dành cả cuộc đời để cố chứng minh định lý phát biểu nghe có vẻ hết sức đơn giản này.
Hành trình mấy trăm năm để giải lời thách đố, cùng với sự phức tạp của lời giải hàng trăm trang, từ bao thế hệ các nhà toán học đã làm người ta vừa nghi ngờ dòng ghi chú của Fermat, vừa tò mò, thán phục ông.
Trong lịch sử công cuộc tìm lời giải cho "Định lý cuối cùng của Fermat" có người phải tự tử và có những người tự lừa chính mình. Cuối cùng sau gần 4 thế kỷ, nhà toán học người Anh, Andrew Wiles cũng công bố lời giải độc nhất vô nhị vào mùa hè năm 1993 và bản chỉnh sửa cuối cùng vào năm 1995, với lời giải dài 200 trang.
Trung tâm Thông tin Tư liệu/TTXVN
Andrew Wiles bên cạnh định lý cuối cùng của Fermat. Ảnh Charles Rex Arbogast/AP.
Giải thưởng được công bố vào ngày 15 tháng ba năm nay và Andrew Wiles đã hoàn toàn ngạc nhiên khi biết tin.
Việc giải quyết được một vấn đề mà nhiều người coi là vô cùng hóc búa – mà phát biểu lại quá đơn giản – đã đưa Wiles trở thành “nhà toán học nổi tiếng bậc nhất của thế kỷ 20”, giám đốc của Viện Toán học Oxford (vốn được đặt trong một tòa nhà mang tên Wiles), Martin Bridson phát biểu. Mặc dù Wiles đã đạt thành tựu này được hơn hai mươi năm, câu chuyện của ông vẫn tiếp tục truyền cảm hứng cho những người trẻ, điển hình là chuyện các học sinh trung học vẫn tới nghe bài giảng đại chúng của ông. “Chúng coi ông ấy như một ngôi sao nhạc rock”, “Chúng xếp hàng để chờ chụp ảnh cùng Wiles”, Bridson kể.
Câu chuyện của Wiles đã thành một truyện truyền kỳ về sự dẻo dai và bền bỉ. Khi còn ở trường Đại học Princeton vào thập niên 80 thế kỷ trước, ông bắt đầu một chuyến độc hành dài bảy năm, tìm kiếm lời giải cho vấn đề này, làm việc trên gác mái mà không ai khác biết ngoài vợ ông. Ông đã tiếp tục cho tới khi đưa ra một thông báo lịch sử tại một hội thảo ở quê nhà Cambridge, Anh vào tháng sáu năm 1993. Không may hai tháng sau, người ta phát hiện ra trong chứng minh của ông có một lỗi sai nghiêm trọng. Nhưng sau một năm làm việc điên cuồng cùng sự trợ giúp của một học trò cũ của mình là Richard Taylor – hiện đang là giáo sư tại Viện nghiên cứu cấp cao Princeton – ông đã có thể “vá” lại chứng minh. Khi kết quả là hai bài báo được công bố vào năm 1995, và chúng chiếm trọn một số của tờ Annals of Mathematics.
Nhưng sau khi khẳng định ban đầu của Wiles chiếm trọn trang nhất của báo chí trên khắp thế giới, áp lực cứu lấy công trình của mình gần như đã làm tê liệt nhà toán học nhút nhát. “Làm toán trong tình trạng phơi bày trước mắt mọi người thế này không phải phong cách của tôi, và tôi không mong muốn phải lặp lại nữa,” Wiles nói trong một bộ phim tài liệu của BBC năm 1996, vẫn còn run rẩy vì trải nghiệm đó. “Gần như không thể tin nổi rằng ông ấy lại có thể vá được chứng minh” ở thời điểm đó, John Rognes, nhà toán học ở trường Đại học Oslo, thành viên hội đồng giải thưởng Abel, cho biết.
“Đã rất, rất căng thẳng”, Wile nói. “Thật bất hạnh rằng con người chúng ta thành công từ những phép thử và những sai sót. Thất bại là mẹ thành công”.
Wiles biết đến nhà toán học Pháp Pierre de Fermat lần đầu tiên khi còn là một đứa trẻ ở Cambridge. Ông được kể lại rằng Fermat đã phát biểu định lý mang tên mình ở dạng viết tay trên lề của một cuốn sách vào năm 1637 (bằng tiếng Latin): “Tôi đã tìm ra một chứng minh tuyệt vời cho định lý này nhưng lề sách quá chật để ghi lại”.
“Tôi tin đây là một câu chuyện rất lãng mạn,” Wiles nói về ý tưởng của Fermat. “Mẫu câu chuyện này lôi cuốn trí tưởng tượng của người ta khi còn trẻ và muốn bước chân vào thế giới toán học.”
Mặc dù khi ấy Fermat đã nghĩ rằng ông chứng minh được nó, nhưng chỉ một chứng minh cho trường hợp đặc biệt n=4 là còn sót lại. Một thế kỷ sau, Leonhard Euler chứng minh nó cho trường hợp n=3 và công trình của Sophie Germain mang lại chứng minh cho vô hạn các lũy thừa, nhưng vẫn không phải cho tất cả. Các chuyên gia bắt đầu có ý cho rằng để giải quyết trường hợp tổng quát phát biểu trong định lý phải cần đến những công cụ toán học mà chỉ đến thế kỷ 20 mới xuất hiện.
Năm 1983, nhà toán học người Đức, Gerd Faltings, hiện đang làm việc tại Viện Toán học Max Planck ở Bonn, đã tiến một bước rất dài với chứng minh rằng phương trình Fermat cùng lắm chỉ có hữu hạn nghiệm, tuy nhiên ông vẫn chưa thể chỉ ra con số đó phải bằng 0. (Thực tế, ông đã chứng minh được một kết quả mà theo các chuyên gia nhận định là sâu sắc và thú vị hơn định lý cuối cùng của Fermat, nó chỉ ra rằng một lớp rộng hơn các phương trình, có cùng lắm là hữu hạn nghiệm).
Để đưa số nghiệm về không, Wiles đã tiếp cận vấn đề theo một hướng khác: ông chứng minh giả thuyết Shimura-Taniyama, một giả thuyết ra đời những năm 50 thế kỷ trước, miêu tả sự tương đương của hai khái niệm khác nhau của toán học, các đường cong elliptic và các dạng modular. Kết quả từ những nhà toán học khác cho thấy rằng chứng minh được tính tương đương này sẽ giúp suy ra định lý cuối cùng của Fermat – và giống như kết quả của Falting, hầu hết các nhà toán học coi kết quả này là sâu sắc và phong phú hơn chính định lý Fermat. (Toàn văn thông cáo giải thưởng Abel viết “giải thưởng trao cho Wiles vì chứng minh tuyệt diệu của ông cho định lý cuối cùng của Fermat bằng cách sử dụng giả thuyết modular cho các đường cong elliptic nửa ổn định, mở ra một kỷ nguyên mới trong lý thuyết số.”)
Mối liên hệ giữa giả thuyết Shimura-Taniyama và định lý cuối cùng của Fermat được đề xuất lần đầu tiên vào năm 1984 bởi nhà toán học Gerhard Frey, hiện đang làm việc ở Đại học Duisburg-Essen, Đức. Ông đã khẳng định rằng bất kỳ phản ví dụ nào cho định lý cuối cùng của Fermat cũng sẽ dẫn tới một phản ví dụ cho giả thuyết Shimura-Taniyama.
Kenneth Ribet, nhà toán học ở Đại học California, Berkeley, đã nhanh chóng chứng minh được rằng khẳng định của Frey là chính xác và bởi vậy nếu ai đó chứng minh được giả thuyết này sẽ giải quyết được định lý cuối cùng của Fermat. Dẫu vậy, vấn đề vẫn không đơn giản hơn đi chút nào. “Andrew Wiles có lẽ là một trong số ít người trên Trái đất đủ can đảm để mơ ước rằng ông có thể tiến lên và chứng minh giả thuyết này, “ Ribet trả lời phỏng vấn trong bộ phim tài liệu của BBC vào năm 1996.
Định lý cuối cùng của Fermat cũng có liên hệ với một kết quả sâu sắc khác trong lý thuyết số, có tên gọi là giả thuyết abc, Rognes bình luận. Nhà toán học Shinichi Mochizuki ở Viện nghiên cứu Toán học, Đại học Kyoto, Nhật Bản đã khẳng định rằng ông đã chứng minh giả thuyết này vào năm 2012, mặc dù bản nháp chứng minh dài 500 trang của ông vẫn đang được bình duyệt bởi các đồng nghiệp. Một số nhà toán học nói rằng công trình của Mochizuki có thể cung cấp một cách thức khác để chứng minh định lý cuối cùng của Fermat, mặc dù Wiles nói rằng ông vẫn hoài nghi về kỳ vọng đó.
Wiles đã giúp tổ chức một hội thảo về công trình của Mochizuki ở Oxford, tháng 12 năm ngoái, mặc dù mối quan tâm trong nghiên cứu của ông tương đối khác. Gần đây, ông tập trung nỗ lực vào một giả thuyết mở quan trọng khác trong lý thuyết số, được liệt kê trong danh sách các vấn đề treo giải Thiên niên kỷ của Viện Toán học Clay tại Oxford, Anh. Ông vẫn tiếp tục làm việc chăm chỉ và tư duy về toán học trong hầu hết thời gian thức của mình, ngay cả khi đi bộ đến văn phòng vào buổi sáng. “Ông ấy không muốn đạp xe,” Bridson nói. “Ông nghĩ rằng sẽ tương đối nguy hiểm nếu vừa đạp xe vừa nghĩ về toán học.”
Hoàng Mai tổng hợp
Phùng Hồ Hải hiệu đính Francs để chơi trò chơi tung đồng xu và lấy tiền đi ăn tối. Nếu mặt ngửa xuất hiện, Fermat được
Francs để chơi trò chơi tung đồng xu và lấy tiền đi ăn tối. Nếu mặt ngửa xuất hiện, Fermat được 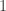 điểm, nếu mặt sấp xuất hiện, Pascal sẽ được một điểm. Ai nhận được
điểm, nếu mặt sấp xuất hiện, Pascal sẽ được một điểm. Ai nhận được 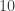 điểm thì trò chơi sẽ kết thúc và người đó sẽ nhận toàn bộ
điểm thì trò chơi sẽ kết thúc và người đó sẽ nhận toàn bộ  Francs. Nhưng một điều bất ngờ đã xảy ra. Khi Fermat được
Francs. Nhưng một điều bất ngờ đã xảy ra. Khi Fermat được 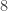 điểm và Pascal được
điểm và Pascal được  điểm
thì Fermat nhận được tin là có một người bạn của anh ấy ốm nặng. Người
báo tin đồng ý sẽ đưa Fermat cùng về Toulouse nhưng với điều kiện Fermat
phải về ngay lập tức. Khi Fermat trở lại Toulouse thì một vấn đề nảy
sinh: Làm thế nào để chia số tiền
điểm
thì Fermat nhận được tin là có một người bạn của anh ấy ốm nặng. Người
báo tin đồng ý sẽ đưa Fermat cùng về Toulouse nhưng với điều kiện Fermat
phải về ngay lập tức. Khi Fermat trở lại Toulouse thì một vấn đề nảy
sinh: Làm thế nào để chia số tiền  Francs?
Francs?
Và trong một bức thư gửi Pascal sau này, Fermat đã nêu cách giải quyết như sau:
Tôi (Fermat) chỉ cần điểm nữa là thắng cuộc chơi, trong khi đó bạn (Pascal) cần thêm
điểm nữa là thắng cuộc chơi, trong khi đó bạn (Pascal) cần thêm 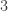 điểm, nên ta cần tung đồng xu tối đa thêm bốn lần nữa thì cuộc chơi sẽ
kết thúc. Trong bốn lần tung này, nếu bạn không nhận được đủ
điểm, nên ta cần tung đồng xu tối đa thêm bốn lần nữa thì cuộc chơi sẽ
kết thúc. Trong bốn lần tung này, nếu bạn không nhận được đủ 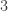 điểm, đồng nghĩa với việc tôi sẽ có thêm
điểm, đồng nghĩa với việc tôi sẽ có thêm  điểm và sẽ dành chiến thắng. Nếu ký hiệu mặt ngửa bởi
điểm và sẽ dành chiến thắng. Nếu ký hiệu mặt ngửa bởi 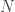 và mặt sấp bởi
và mặt sấp bởi 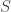 , thì có tất cả
, thì có tất cả  kết quả có thể xảy ra sau đây:
kết quả có thể xảy ra sau đây:

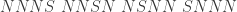


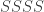 .
.
Vì trong kết quả trên, có
kết quả trên, có  kết quả thuận lợi cho tôi. Do đó,
kết quả thuận lợi cho tôi. Do đó,  Francs cần được chia theo tỉ lệ
Francs cần được chia theo tỉ lệ 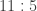 nghiêng về phía tôi, nghĩa là, tôi sẽ nhận
nghiêng về phía tôi, nghĩa là, tôi sẽ nhận  Francs, và bạn sẽ nhận
Francs, và bạn sẽ nhận  Francs.
Francs.
Pascal rất hài lòng với cách giải quyết của Fermat. Tuy nhiên, Pascal nhận thấy phương pháp liệt kê tất cả các trường hợp có thể xảy ra của Fermat tương đối tẻ nhạt đối với bài toán tổng quát. Pascal đã lý luận như sau: Trong lời giải của Fermat, ta nhận thấy nếu có hoặc hơn
hoặc hơn  mặt ngửa xuất hiện thì Fermat sẽ thắng cuộc. Số các kết quả có hai mặt ngửa khi tung đồng xu
mặt ngửa xuất hiện thì Fermat sẽ thắng cuộc. Số các kết quả có hai mặt ngửa khi tung đồng xu  lần là
lần là  . Như vậy, số các trường hợp thuận lợi cho Fermat là
. Như vậy, số các trường hợp thuận lợi cho Fermat là
 .
.
Đây chính là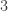 số hạng đầu tiên trong dòng thứ năm trong tam giác Pascal:
số hạng đầu tiên trong dòng thứ năm trong tam giác Pascal:



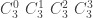

Đối với bài toán tổng quát, khi người chơi thứ nhất và người thứ hai lần lượt cần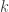 và
và 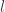 điểm nữa để dành phần thắng, thì số tiền sẽ chia cho người thứ nhất theo tỉ lệ
điểm nữa để dành phần thắng, thì số tiền sẽ chia cho người thứ nhất theo tỉ lệ  , trong đó $latex $ là tổng số
, trong đó $latex $ là tổng số 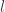 số hạng đầu tiên của dòng thứ
số hạng đầu tiên của dòng thứ  trong tam giác Pascal, còn
trong tam giác Pascal, còn 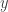 là tổng của tất cả các số hạng trong dòng đó:
là tổng của tất cả các số hạng trong dòng đó:
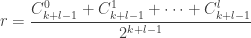 .
.
Trở lại trò chơi của Fermat và Pascal , số tiền chia cho Fermat theo tỉ lệ
, số tiền chia cho Fermat theo tỉ lệ

Cho dù lý luận trên của Fermat và Pascal tương đối đơn giản đối với chúng ta ngày nay, nhưng nó là một cuộc cách mạng vào những năm giữa thế kỷ 17. Đó chính là cách định nghĩa xác suất theo quan điểm cổ điển. Khi một phép thử ngẫu nhiên có kết quả đồng khả năng (equally probable outcomes), trong đó có
kết quả đồng khả năng (equally probable outcomes), trong đó có 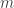 kết quả thuận lợi cho sự kiện
kết quả thuận lợi cho sự kiện  , thì xác suất của biến cố
, thì xác suất của biến cố  được định nghĩa
được định nghĩa

Trong bài toán chia điểm của Fermat và Pascal, có kết quả đồng khả năng có thể xảy ra khi tung một đồng xu cân đối
kết quả đồng khả năng có thể xảy ra khi tung một đồng xu cân đối  lần, trong đó có
lần, trong đó có  kết quả thuận lợi cho sự kiện
kết quả thuận lợi cho sự kiện  (sự kiện Fermat thắng cuộc). Vậy
(sự kiện Fermat thắng cuộc). Vậy

Bài tập: Hãy trình bày cách chia tiền thưởng trong trường hợp Fermat được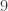 điểm và Pascal được
điểm và Pascal được 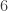 điểm thì trò chơi bị dừng lại.
điểm thì trò chơi bị dừng lại.
44-Leonard Euler

1707-1783
Thụy Sĩ
Vật Lý, Toán Học
Euler với lý thuyết số
Số hoàn hảo
Ngay từ thời của Pythagoras (thế kỷ thứ 6 trước Công nguyên) câu hỏi đặt ra với các số hoàn hảo đã được biết tới.
Định nghĩa số hoàn hảo: Số hoàn hảo là một số nguyên dương mà tổng các ước thực sự của nó bằng chính nó.
Ví dụ: Các ước thực sự của 6 là 1,2,3 và 6=1+2+3.
Trong quá trình nghiên cứu về số hoàn hảo, Euler đã đưa ra một số khái niệm và các khái niệm này đều có những đóng góp to lớn không chỉ cho riêng việc nghiên cứu các số hoàn hảo.
Định nghĩa: σ (n) là tổng các ước nguyên dương của n. (Ban đầu Euler sử dụng kí hiệu ∫(n), ngày nay kí hiệu đó được sử dụng cho tích phân.)
Euler cũng đưa chứng minh nhiều khẳng định liên quan tới σ (n).
Mệnh đề: Nếu n là một số hoàn hảo thì σ (n) = 2n.
Định lý: Nếu n là một số hoàn hảo chẵn thì n = 2k-1 (2k-1) và 2k -1 là một số nguyên tố.
Với định lý nêu trên, Euler đã chỉ ra dạng của các số hoàn hảo chẵn, nhưng như vậy vẫn là chưa đủ cho bộ óc vĩ đại của mình, năm 1747 trong một bài báo của mình, Euler đã đưa ra câu hỏi “Liệu có số hoàn hảo nào là số lẻ?” Sau đó, ông gọi đó là vấn đề khó nhất. Vào thời điểm đó tất cả mọi người đều tin rằng đó là một vấn đề thực sự khó, vì ngay cả Euler cũng xác nhận điều đó.
Cho đến ngày nay, vấn đề về sự tồn tại của một số hoàn hảo lẻ vẫn còn là một thách thức cho tất cả các nhà toán học. Họ vẫn chưa thể khẳng định được sự tồn tại của số hoàn hảo lẻ. Ngay cả với sự trợ giúp của các hệ thống siêu máy tính thì câu hỏi trên vẫn là một câu hỏi mở. Có rất nhiều người đã tham gia nghiên cứu vấn đề này và cũng cho ra nhiều kết quả thú vị.
* Một số hoàn hảo lẻ không thể chia hết cho 105.
* Số hoàn hảo lẻ nhỏ nhất lớn hơn 10300
* Một số hoàn hảo lẻ có ít nhất ba thừa số nguyên tố khác nhau.
* Tổng nghịch đảo của các số hoàn hảo lẻ là hữu hạn.
Đây là một điều rất thú vị bởi trong giải tích thì không hội tụ, nhưng nếu chỉ lấy trên tập các số hoàn hảo lẻ thì nó lại hữu hạn.
không hội tụ, nhưng nếu chỉ lấy trên tập các số hoàn hảo lẻ thì nó lại hữu hạn.
Hi vọng trong tương lai gần các nhà Toán học sẽ có câu trả lời cho vấn đề “số hoàn hảo lẻ”.
Số nguyên tố và hàm Zeta
Bắt đầu với bài toán Basel tính tổng nghịch đảo các bình phương

Tổng quát hoá tổng trên ta được hàm Zeta
Euler đã tính được bằng cách xét đa thức
bằng cách xét đa thức

sau đó Euler viết P(x) dưới 2 dạng khác nhau và đồng nhất hệ số để tính được ζ (2).

Xét hệ số của x2 trong P(x) nói trên, ta có:

Và cuối cùng thu được
Không dừng lại ở đó, Euler còn tính được kết quả tổng quát .

Trong đó |B2n| là số Bernoulli
Euler gặp khó khăn với trường hợp s lẻ và ông không tin nó có liên quan tới . Ngày nay thì đây cũng là một câu hỏi mở đang chờ được các nhà toán học giải đáp.
. Ngày nay thì đây cũng là một câu hỏi mở đang chờ được các nhà toán học giải đáp.
Trong quá trình tính toán với các bài toán trên, Euler đã đưa ra rất nhiều đẳng thức bất ngờ và nhiều điểm độc đáo, sau này trở thành các công cụ tính toán mạnh cho nhiều nhà toán học. Với lý thuyết số, Euler còn chứng minh rất nhiều định lý quan trọng trong lý thuyết đồng dư, số nguyên tố, số Mersenne… do khuôn khổ bài viết nên tôi chỉ trình bày sơ lược các kết quả đại diện trong các lĩnh vực mà Euler để lại.
Euler và định lý cơ bản của đại số
Định lý: Mọi đa thức bậc n với hệ số phức luôn phân tích được thành n nhân tử tuyến tính
Đây là định lý cơ bản của đại số, một trong những định lý quan trọng nhất và được sử dụng rộng rãi không chỉ riêng trong đại số. Các chứng minh của định lý này cho đến nay vẫn chưa có một chứng minh nào là thuần tuý đại số, các chứng minh đã có đều mang chút ít màu sắc của giải tích phức.
Năm 1794, Euler cũng đưa ra một phác thảo chứng minh cho định lý cơ bản của đại số. khi đó Euler mới chỉ cụ thể hoá được trường hợp bậc 4.
Định lý Euler-Fermat và Mật mã
Định lý: Nếu a và n là hai số nguyên tố cùng nhau thì aφ(n) ≡ 1 (mod n). Với φ(n) là phi hàm Euler.
Trong mật mã, ta quan tâm tới việc truyền thông tin một cách an toàn từ người gửi tới người nhận. Một thông điệp M được mã hoá thành E và người nhận sẽ giải mã từ E thu được M. Sẽ rất thuận tiện nếu mỗi kí tự trong bảng mã ASCII được thay thế bằng các số tự nhiên, khi đó việc biến M → E sẽ chuyển sang ngôn ngữ ánh xạ f : N → N. Vấn đề ta phải tìm một hàm f thoả mãn:
- f là một song ánh
- f có công thức và khó tìm được nghịch ảnh của f.
Một giải pháp cho vấn đề này là chương trình mã hóa RSA đang được sử dụng rộng rãi (đặt theo tên nhà phát minh của nó R. Rivet, A. Shamir và Adleman L.)
Tạo Mã và Mã hoá
* Chọn hai số nguyên tố p,q lớn và khác nhau.
* Tính n = p.q
* Tính giá trị của φ(n) = (p-1) (q-1)
* Chọn 1 số nguyên tố e thoả mãn: 1
* Tìm d: (d.e) ≡ 1 mod (φ(n))
Mã công khai là n, module và e số mũ công khai, mã bí mật

Người gửi chuyển thông tin M thành số m2
mod (n)
Bánh răng Euler
Trong quá trình làm việc với thiết kế tua bin nước, Euler đã tối ưu cho
các bánh răng để giảm sức lao động, giảm tiếng ồn… Euler không chỉ là
người phát minh ra mà còn dự đoán được cả quỹ đạo chuyển động của nó.
Bánh răng này được gọi là bánh răng – Euler. Sau này người ta còn gọi đó
là phương trình Euler–Savary.
Đĩa Euler
Euler cũng nghiên cứu tới chuyện động của các vật thể xoay quanh một trục, có tính tới ma sát. Một ví dụ thú vị là đĩa Euler, một đĩa tròn (đồng nhất) bằng kim loại được quay trên một bề mặt mịn sạch. Lúc đầu, nó sẽ xoay xung quanh trục thẳng đứng của nó, nhưng do ma sát, trục đang bắt đầu nghiêng và đĩa để cuộn trên một đường tròn. Càng ngày trục nghiêng càng bị nghiêng dần, các vòng tròn thì ngày một rộng ra. Dù có xét đến yếu tố nào đi nữa thì quả bóng vẫn sẽ dừng lại.
Chìa khóa để giải thích chuyển động này là phương trình Euler, một tập hợp các phương trình vi phân liên quan đến các góc Euler và các thông số khác. Các chi tiết kỹ thuật của các chuyển động, vẫn còn được tiếp tục nghiên cứu cho tới tận bây giờ.
Lý thuyết đồ thị và Tôpô
Con sông Pregel, chảy qua thành phố Phổ Königsberg, chia thành phố thành một hòn đảo và ba vùng đất riêng biệt, một ở phía Bắc, một ở phía Đông, và một ở phía Nam. Có tất cả bảy cây cầu, sắp xếp như trong bản đồ với các điểm màu xanh lá cây.
Bài toán: người ta có thể đi dạo từ một điểm ở thành phố khác bằng cách đi qua mỗi cây cầu đúng một lần? Bậc của một đỉnh là cạnh nối với nó; trong đồ thị các cây cầu Königsberg, ba nút có bậc bằng 3 và một nút có bậc 5. Euler đã chứng minh rằng một chu trình có dạng như mong muốn chỉ tồn tại khi và chỉ khi không có nút bậc lẻ. Một đường đi như vậy được gọi là một chu trình Euler. Do đồ thị các cây cầu Königsberg có bốn nút bậc lẻ, nên nó không thể có chu trình Euler.
Lời giải của Euler cho bài toán trên là cơ sở cho nền móng của Topo học. (Xem thêm bài viết của Nguyễn Hữu Việt Hưng trên Tia Sáng số 6 - 20/3/2016.)
Công thức Euler
Với mọi số thực x ta luôn có: eix = cos x + i.sin x . Với e là số vô tỉ được tính qua giới hạn

công thức Euler là phổ biến trong toán học, vật lý và kỹ thuật. Nhà vật lý Richard Feynman được gọi là phương trình “viên ngọc quý” và “công thức đáng chú ý nhất trong toán học.”
Một công thức tương đương là ix= ln (cos x + i sin x), công thức này được đưa ra bởi Cotes (1714). Công thức Euler được sử dụng trong rất nhiều lĩnh vực của Toán từ lý thuyết số phức, phương trình vi phân,…từ đơn giản nhất cho đến phức tạp.
Qua ba bài viết, chúng ta đã cùng có một hành trình xuyên suốt cuộc đời và sự nghiệp của nhà Toán học vĩ đại Euler, một người thầy vĩ đại bởi tất cả những gì ông để lại đã trực tiếp hoặc gián tiếp tạo nên bộ mặt khoa học và cuộc sống ngày nay.
Nhân dịp kỷ niệm ngày sinh của Leonard Euler-Bài giảng toán học cung cấp một vài thông tin về nhà toán học tài ba này.




45-Alessandro Volta

1745-1827
Ý
Vật Lý, Hóa Học

Alexandro Volta (18/2/1745 - 5/5/1827)

Chân dung Volta, cha đẻ của pin điện



Ngày nay, mô hình pin Volta vẫn được bảo tồn
43-Pierre de Fermat
1601-1665
Pháp
Toán Học
Pierre de Fermat, luật sư cực "đỉnh" môn toán
Logo Google ngày hôm nay nói về một luật sư nhưng lại cực kì "siêu" toán đấy các bạn ạ!
Đã lâu lắm rồi trên trang chủ của Google mới lại
xuất hiện hình ảnh Google Doodle trong ngày. Vậy hình tấm bảng trên
trang chủ Google ngày 17/8/2011 có ý nghĩa gì các bạn nhỉ? Chúng mình
cùng nhau tìm hiểu nhé!
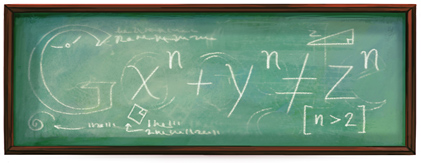
Logo Google ngày hôm nay là một tấm bảng với những phép toán bí ẩn
Thì ra tấm bảng đó kể về Pierre de
Fermat (1601-1665) là một học giả nghiệp dư vĩ đại, một nhà toán học nổi
tiếng và là cha đẻ của lý thuyết số hiện đại. Sinh ra vào ngày 17 tháng
8 năm 1601 tại Beaumont-de-Lomagne, Pháp. Ông xuất thân trong một gia
đình khá giả, học ở Toulouse và lấy bằng cử nhân luật dân sự rồi
sau đó làm chánh án.

Chỉ trừ gia đình cùng những người bạn thân, chẳng
ai hay biết ông đam mê môn toán học. Mãi sau khi Pierre de Fermat mất
vào ngày 12 tháng 1 năm 1665 tại Castres, Pháp, người con trai ông là
Samuel de Fermat (1630-1690) mới in dần các công trình của cha kể từ năm
1670. Cùng thời với Pierre de Fermat còn có một nhà toán học khác là
Blaise Pascal cũng là người mở đầu trong việc nghiên cứu toán học trên
toàn thế giới. Vào năm 1896, các tác phẩm của Fermat được ấn hành thành 4
tập dày. Qua đó, người đọc vô cùng ngạc nhiên và khâm phục trước sự
đóng góp to lớn của ông. Chính ông là người sáng lập nên lý thuyết số
hiện đại, trong đó có 2 định lý nổi bật: định lý nhỏ Fermat và định lý
lớn Fermat (định lý cuối cùng của Fermat).

Trong hình học, ông phát triển ra phương pháp tọa độ,
lập phương trình đường thẳng và các đường cong bậc hai rồi chứng minh
rằng các đường cong nọ chính là các thiết diện cônic. Trong toán giải
tích, ông nêu các quy tắc lấy đạo hàm của hàm mũ với số mũ bất kỳ, tìm
cực trị, tính tích phân những hàm mũ với số mũ phân số và số mũ
âm. Không những chỉ về toán, nguyên lý Fermat về truyền sáng
lại của ông một định luật khá quan trọng trong quang học. Quả thật ông
là một người có quá nhiều đóng góp cho nền toán học cũng như vật lý thế
giới.
Dù hoạt động khoa học kiên trì và giàu nhiệt huyết,
đem lại nhiều thành quả to lớn đến cho ông. Thế nhưng éo le thay,
Pierre de Fermat chẳng thể nào lấy việc nghiên cứu toán làm nghề chính
thức của ông.

Những dòng ước nguyện cuối cùng của Fermat.
Câu chuyện về định lý cuối cùng của Fermat là câu chuyện độc nhất vô nhị trong lịch sử toán học thế giới, khởi nguồn từ cổ đại với nhà toán học Pythagore. Bài toán cuối cùng của Fermat (sau này giới toán học gọi là Định lý cuối cùng của Fermat, hay Định lý lớn Fermat) có gốc từ định lý Pythagore: “Trong tam giác vuông thì bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông”. Và Fermat thay đổi phương trình Pythagore sau đó tạo ra một bài toán "siêu khó" đến mức bất hủ.
Sau đây là những nghiên cứu của ông:
Định lý nhỏ Fermat:
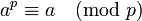
Với p là một số nguyên tố khác 2 thì chia một số a mũ p cho p sẽ có số dư chính bằng a.
Định lý lớn Fermat
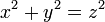
Xét phương trình Pythagore:
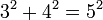
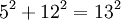
Với phương trình này có vô số bộ nghiệm thỏa mãn điều kiện:
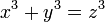
Và ông tự đặt câu hỏi: "Liệu có thể tìm được nghiệm (nguyên) cho phương trình bậc ba này hay không?"
Ông khẳng định là không. Thực ra, ông khẳng định điều đó cho phương trình tổng quát:

Trong đó nếu n luôn lớn hơn 2 thì không thể tìm được nghiệm (nguyên) nào. Đó chính là Định lý Fermat cuối cùng.
Điều lý thú ở đây là phỏng đoán này được Fermat ghi
bên lề một cuốn sách mà không hề được chứng minh, thế nhưng ông không
quên kèm theo dòng chữ: “Tôi có một phương pháp rất hay để chứng minh cho trường hợp tổng quát, nhưng không thể viết ra đây vì lề sách quá hẹp”.
Các nhà toán học đã cố gắng giải bài toán này trong
suốt 300 năm qua. Trong lịch sử công cuộc tìm lời giải cho "Định lý
cuối cùng của Fermat" có người phải tự tử và có những người tự lừa chính
mình (do ngộ nhận trong toán học). Và cuối cùng, nhà toán học Andrew
Wiles (Người Mỹ gốc Anh) sau 7 năm làm việc trong cô độc và hơn 1 năm
giày vò trong cô đơn cuối cùng cũng công bố lời giải độc nhất vô nhị vào
mùa hè năm 1993 và bản chỉnh sửa cuối cùng vào năm 1995, lời giải của
Andrew dài tới tận 200 trang cơ đấy các bạn ạ!
Fermat và Định lý Lớn thách đố suốt 4 thế kỷ
Nhắc đến Pierre de Fermat là nhắc đến một nhà toán học vĩ đại người Pháp. Ông là cha đẻ của lý thuyết số hiện đại, trong đó có hai định lý nổi tiếng: định lý nhỏ Fermat và định lý lớn Fermat hay còn gọi là định lý cuối cùng của Fermat.Pierre de Fermat sinh ngày 17/8/1601 tại Beaumont-de-Lomagne, Pháp trong một gia đình khá giả. Ông học ở Toulouse về luật dân sự, sau đó làm chánh án. Tuy vậy, Fermat lại vô cùng say mê toán học với thói quen nổi tiếng là ghi các ghi chú bên lề các quyển sách.

Nhà toán học Pierre de Fermat.
|
Nhà nghiên cứu lịch sử toán học nổi tiếng E.T.Bell đã từng gọi Fermat là "Hoàng tử của những người nghiệp dư". Bell cho rằng Fermat đã đạt được nhiều thành tựu toán học quan trọng hơn hầu hết các nhà toán học "chuyên nghiệp" cùng thời với ông.
Fermat rất say mê các công trình toán học của người Hy Lạp cổ đại, chính các công trình như Archimedes và Eudoxus đã gợi ý cho Fermat xây dựng khái niệm các phép toán giải tích.
Ông cố gắng tổng quát hóa các công trình toán học cổ điển và tìm ra nét mới trong kho tàng các phát minh đã bị chôn vùi từ rất lâu, như ông đã từng nói: "Tôi đã tìm được rất nhiều định lý đẹp vô cùng".
Mãi sau khi Fermat mất (12/1/1665), con trai ông mới in dần các công trình của cha kể từ năm 1670. Đến năm 1896, hầu hết các tác phẩm của Fermat được ấn hành thành 4 tập dày. Người ta đã vô cùng ngạc nhiên và khâm phục trước sự đóng góp lớn lao của ông.
Trong hình học, Fermat phát triển ra phương pháp tọa độ, lập phương trình đường thẳng và các đường cong bậc hai rồi chứng minh rằng các đường cong nọ chính là các thiết diện cônic. Trong toán giải tích, ông nêu các quy tắc lấy đạo hàm của hàm mũ với số mũ bất kỳ, tìm cực trị, tính tích phân những hàm mũ với số mũ phân số và số mũ âm.
Trong vật lý, chúng ta quá quen thuộc nguyên lý Fermat về truyền sáng, đó là một định luật quan trọng của quang học.
Nhưng đóng góp quan trọng nhất trong toán học của Fermat là lý thuyết số hiện đại, trong đó có 2 định lý nổi bật: định lý nhỏ Fermat và định lý lớn Fermat (định lý cuối cùng của Fermat).
Câu chuyện về định lý cuối cùng của Fermat là câu chuyện độc nhất vô nhị trong lịch sử toán học thế giới, khởi nguồn từ cổ đại với nhà toán học Pythagore.
Bài toán cuối cùng (sau này giới toán học gọi là Định lý cuối cùng của Fermat, hay Định lý lớn Fermat) có gốc từ định lý Pythagore: "Trong một tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông". Fermat thay đổi phương trình Pythagore và tạo ra một bài toán khó bất hủ.
Xét phương trình Pythagore: x2 + y2 = z2
Người ta có thể hỏi những nghiệm số nguyên của phương trình này là gì, và có thể thấy rằng: Có vô số nghiệm nguyên chẳng hạn (3,4,5) và (5,12,13).
Fermat khi đó xét dạng bậc ba của phương trình này: x3 + y3 = z3.
Đối với câu hỏi có thể tìm được nghiệm (nguyên) cho phương trình bậc ba này hay không? Fermat đã khẳng định là không. Thực ra, ông khẳng định điều đó cho họ phương trình tổng quát : xn + yn = zn với n là số nguyên lớn hơn 2. Đó là Định lý Fermat cuối cùng.
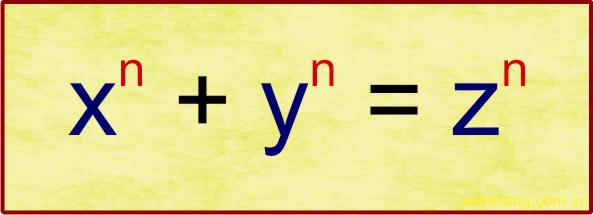 |
Gắn liền với định lý này là câu chuyện rất hay, đó là Fermat cho rằng không thể tìm được nghiệm (nguyên) cho phương trình bậc ba. Điều lý thú ở đây là phỏng đoán này được Fermat ghi bên lề một cuốn sách mà không chứng minh, nhưng có kèm theo dòng chữ: “Tôi có một phương pháp rất hay để chứng minh cho trường hợp tổng quát, nhưng không thể viết ra đây vì lề sách quá hẹp.”
Với những dòng viết tay đó, nhà toán học người Pháp Pierre de Fermat đã chính thức buông lời thách đố đối với thế hệ các nhà toán học sau ông. Nhiều nhà toán học đã dành cả cuộc đời để cố chứng minh định lý phát biểu nghe có vẻ hết sức đơn giản này.
Hành trình mấy trăm năm để giải lời thách đố, cùng với sự phức tạp của lời giải hàng trăm trang, từ bao thế hệ các nhà toán học đã làm người ta vừa nghi ngờ dòng ghi chú của Fermat, vừa tò mò, thán phục ông.
Trong lịch sử công cuộc tìm lời giải cho "Định lý cuối cùng của Fermat" có người phải tự tử và có những người tự lừa chính mình. Cuối cùng sau gần 4 thế kỷ, nhà toán học người Anh, Andrew Wiles cũng công bố lời giải độc nhất vô nhị vào mùa hè năm 1993 và bản chỉnh sửa cuối cùng vào năm 1995, với lời giải dài 200 trang.
Trung tâm Thông tin Tư liệu/TTXVN
Andrew Wiles - Nhà toán học nổi tiếng bậc nhất thế kỷ 20
04/07/2016 00:00 -
Giải thưởng Abel 2016 được trao cho nhà lý thuyết số
người Anh, Andrew Wiles với chứng minh cho Định lý cuối cùng của Fermat
(còn được biết đến dưới tên gọi định lý lớn Fermat). Định lý này phát
biểu rằng, với mọi n>2, phương trình xn+yn=zn không có nghiệm nguyên
dương. Giải thưởng trao cho Wiles có giá trị 6 triệu kroner (tương đương
700.000$)
Andrew Wiles bên cạnh định lý cuối cùng của Fermat. Ảnh Charles Rex Arbogast/AP.
Giải thưởng được công bố vào ngày 15 tháng ba năm nay và Andrew Wiles đã hoàn toàn ngạc nhiên khi biết tin.
Việc giải quyết được một vấn đề mà nhiều người coi là vô cùng hóc búa – mà phát biểu lại quá đơn giản – đã đưa Wiles trở thành “nhà toán học nổi tiếng bậc nhất của thế kỷ 20”, giám đốc của Viện Toán học Oxford (vốn được đặt trong một tòa nhà mang tên Wiles), Martin Bridson phát biểu. Mặc dù Wiles đã đạt thành tựu này được hơn hai mươi năm, câu chuyện của ông vẫn tiếp tục truyền cảm hứng cho những người trẻ, điển hình là chuyện các học sinh trung học vẫn tới nghe bài giảng đại chúng của ông. “Chúng coi ông ấy như một ngôi sao nhạc rock”, “Chúng xếp hàng để chờ chụp ảnh cùng Wiles”, Bridson kể.
Câu chuyện của Wiles đã thành một truyện truyền kỳ về sự dẻo dai và bền bỉ. Khi còn ở trường Đại học Princeton vào thập niên 80 thế kỷ trước, ông bắt đầu một chuyến độc hành dài bảy năm, tìm kiếm lời giải cho vấn đề này, làm việc trên gác mái mà không ai khác biết ngoài vợ ông. Ông đã tiếp tục cho tới khi đưa ra một thông báo lịch sử tại một hội thảo ở quê nhà Cambridge, Anh vào tháng sáu năm 1993. Không may hai tháng sau, người ta phát hiện ra trong chứng minh của ông có một lỗi sai nghiêm trọng. Nhưng sau một năm làm việc điên cuồng cùng sự trợ giúp của một học trò cũ của mình là Richard Taylor – hiện đang là giáo sư tại Viện nghiên cứu cấp cao Princeton – ông đã có thể “vá” lại chứng minh. Khi kết quả là hai bài báo được công bố vào năm 1995, và chúng chiếm trọn một số của tờ Annals of Mathematics.
Nhưng sau khi khẳng định ban đầu của Wiles chiếm trọn trang nhất của báo chí trên khắp thế giới, áp lực cứu lấy công trình của mình gần như đã làm tê liệt nhà toán học nhút nhát. “Làm toán trong tình trạng phơi bày trước mắt mọi người thế này không phải phong cách của tôi, và tôi không mong muốn phải lặp lại nữa,” Wiles nói trong một bộ phim tài liệu của BBC năm 1996, vẫn còn run rẩy vì trải nghiệm đó. “Gần như không thể tin nổi rằng ông ấy lại có thể vá được chứng minh” ở thời điểm đó, John Rognes, nhà toán học ở trường Đại học Oslo, thành viên hội đồng giải thưởng Abel, cho biết.
“Đã rất, rất căng thẳng”, Wile nói. “Thật bất hạnh rằng con người chúng ta thành công từ những phép thử và những sai sót. Thất bại là mẹ thành công”.
Wiles biết đến nhà toán học Pháp Pierre de Fermat lần đầu tiên khi còn là một đứa trẻ ở Cambridge. Ông được kể lại rằng Fermat đã phát biểu định lý mang tên mình ở dạng viết tay trên lề của một cuốn sách vào năm 1637 (bằng tiếng Latin): “Tôi đã tìm ra một chứng minh tuyệt vời cho định lý này nhưng lề sách quá chật để ghi lại”.
“Tôi tin đây là một câu chuyện rất lãng mạn,” Wiles nói về ý tưởng của Fermat. “Mẫu câu chuyện này lôi cuốn trí tưởng tượng của người ta khi còn trẻ và muốn bước chân vào thế giới toán học.”
Mặc dù khi ấy Fermat đã nghĩ rằng ông chứng minh được nó, nhưng chỉ một chứng minh cho trường hợp đặc biệt n=4 là còn sót lại. Một thế kỷ sau, Leonhard Euler chứng minh nó cho trường hợp n=3 và công trình của Sophie Germain mang lại chứng minh cho vô hạn các lũy thừa, nhưng vẫn không phải cho tất cả. Các chuyên gia bắt đầu có ý cho rằng để giải quyết trường hợp tổng quát phát biểu trong định lý phải cần đến những công cụ toán học mà chỉ đến thế kỷ 20 mới xuất hiện.
Năm 1983, nhà toán học người Đức, Gerd Faltings, hiện đang làm việc tại Viện Toán học Max Planck ở Bonn, đã tiến một bước rất dài với chứng minh rằng phương trình Fermat cùng lắm chỉ có hữu hạn nghiệm, tuy nhiên ông vẫn chưa thể chỉ ra con số đó phải bằng 0. (Thực tế, ông đã chứng minh được một kết quả mà theo các chuyên gia nhận định là sâu sắc và thú vị hơn định lý cuối cùng của Fermat, nó chỉ ra rằng một lớp rộng hơn các phương trình, có cùng lắm là hữu hạn nghiệm).
Để đưa số nghiệm về không, Wiles đã tiếp cận vấn đề theo một hướng khác: ông chứng minh giả thuyết Shimura-Taniyama, một giả thuyết ra đời những năm 50 thế kỷ trước, miêu tả sự tương đương của hai khái niệm khác nhau của toán học, các đường cong elliptic và các dạng modular. Kết quả từ những nhà toán học khác cho thấy rằng chứng minh được tính tương đương này sẽ giúp suy ra định lý cuối cùng của Fermat – và giống như kết quả của Falting, hầu hết các nhà toán học coi kết quả này là sâu sắc và phong phú hơn chính định lý Fermat. (Toàn văn thông cáo giải thưởng Abel viết “giải thưởng trao cho Wiles vì chứng minh tuyệt diệu của ông cho định lý cuối cùng của Fermat bằng cách sử dụng giả thuyết modular cho các đường cong elliptic nửa ổn định, mở ra một kỷ nguyên mới trong lý thuyết số.”)
Mối liên hệ giữa giả thuyết Shimura-Taniyama và định lý cuối cùng của Fermat được đề xuất lần đầu tiên vào năm 1984 bởi nhà toán học Gerhard Frey, hiện đang làm việc ở Đại học Duisburg-Essen, Đức. Ông đã khẳng định rằng bất kỳ phản ví dụ nào cho định lý cuối cùng của Fermat cũng sẽ dẫn tới một phản ví dụ cho giả thuyết Shimura-Taniyama.
Kenneth Ribet, nhà toán học ở Đại học California, Berkeley, đã nhanh chóng chứng minh được rằng khẳng định của Frey là chính xác và bởi vậy nếu ai đó chứng minh được giả thuyết này sẽ giải quyết được định lý cuối cùng của Fermat. Dẫu vậy, vấn đề vẫn không đơn giản hơn đi chút nào. “Andrew Wiles có lẽ là một trong số ít người trên Trái đất đủ can đảm để mơ ước rằng ông có thể tiến lên và chứng minh giả thuyết này, “ Ribet trả lời phỏng vấn trong bộ phim tài liệu của BBC vào năm 1996.
Định lý cuối cùng của Fermat cũng có liên hệ với một kết quả sâu sắc khác trong lý thuyết số, có tên gọi là giả thuyết abc, Rognes bình luận. Nhà toán học Shinichi Mochizuki ở Viện nghiên cứu Toán học, Đại học Kyoto, Nhật Bản đã khẳng định rằng ông đã chứng minh giả thuyết này vào năm 2012, mặc dù bản nháp chứng minh dài 500 trang của ông vẫn đang được bình duyệt bởi các đồng nghiệp. Một số nhà toán học nói rằng công trình của Mochizuki có thể cung cấp một cách thức khác để chứng minh định lý cuối cùng của Fermat, mặc dù Wiles nói rằng ông vẫn hoài nghi về kỳ vọng đó.
Wiles đã giúp tổ chức một hội thảo về công trình của Mochizuki ở Oxford, tháng 12 năm ngoái, mặc dù mối quan tâm trong nghiên cứu của ông tương đối khác. Gần đây, ông tập trung nỗ lực vào một giả thuyết mở quan trọng khác trong lý thuyết số, được liệt kê trong danh sách các vấn đề treo giải Thiên niên kỷ của Viện Toán học Clay tại Oxford, Anh. Ông vẫn tiếp tục làm việc chăm chỉ và tư duy về toán học trong hầu hết thời gian thức của mình, ngay cả khi đi bộ đến văn phòng vào buổi sáng. “Ông ấy không muốn đạp xe,” Bridson nói. “Ông nghĩ rằng sẽ tương đối nguy hiểm nếu vừa đạp xe vừa nghĩ về toán học.”
Hoàng Mai tổng hợp
Phùng Hồ Hải hiệu đính
Giải “Nobel Toán học” vinh danh nhà toán học người Anh
Ngày đăng: 09:46 05/04/2016 | Lượt xem: 3329
Andrew
John Wiles, một nhà toán học người Anh, hiện là GS Toán học của Đại học
Princeton (Hoa Kỳ) vừa giành được giải thưởng Abel khi giải đáp thành
công một phương trình toán học đưa ra từ 300 năm trước.
Giải thưởng này được ví là “Nobel Toán học” của thế giới, danh tiếng tương đương với giải Fields, giải thưởng Toán học danh giá thế giới (mà Giáo sư Ngô Bảo Châu từng vinh dự nhận vào năm 2010 - ND). Là giải thưởng của Viện Khoa học và Văn chương Na Uy, giải Abel sẽ được Na Uy trao hàng năm cho những nhà toán học xuất chúng.
 Andrew
Wiles đã giải đáp một vấn đề gây đau đầu cho nhiều nhà toán học suốt
hơn 300 năm qua, đó là “Định lý cuối của Fermat” của nhà toán học người
Pháp Pierre de Fermat đưa ra vào năm 1637. Đây là một trong những định
lý nổi tiếng trong lịch sử toán học.
Andrew
Wiles đã giải đáp một vấn đề gây đau đầu cho nhiều nhà toán học suốt
hơn 300 năm qua, đó là “Định lý cuối của Fermat” của nhà toán học người
Pháp Pierre de Fermat đưa ra vào năm 1637. Đây là một trong những định
lý nổi tiếng trong lịch sử toán học.
Định lý này phát biểu như sau: “Không tồn tại các nghiệm nguyên khác không x, y, và z thỏa mãn xn + yn = zn trong đó n là một số nguyên lớn hơn”.
Fermat viết lại trên lề một cuốn sách rằng ông có cách giải rất hay, nhưng vì lề sách bé quá không đủ chỗ để viết.
Cho tới đầu thế kỷ 20, các nhà toán học chỉ chứng minh định lý này là đúng với n = 3, 4, 5, 7 và các bội số của nó. Nhà toán học người Đức Ernst Kummer đã chứng minh định lý này là đúng với mọi số nguyên tố tới 100 (trừ 3 số nguyên tố phi chính quy là 37, 59, 67).
Mãi đến những năm 1990, Giáo sư Andrew Wiles cuối cũng đã giải quyết được vấn đề sau 8 năm nghiên cứu. Tháng 8/1995, tại một hội thảo của đại học Boston (Hoa Kỳ), ông đã được giới toán học công nhận công trình nghiên cứu của mình ở tuổi 63.
Trong cuộc trả lời phỏng vấn mới đây với tờ báo The Guardian của Anh, ông nói rằng mình tìm thấy định lý này khi mới 10 tuổi. Ông cho biết: “Giải thưởng là một vinh dự to lớn đối với tôi…. phương trình Fermat là niềm đam mê của tôi từ nhỏ và nó luôn thôi thúc tôi phải hoàn thành trong những năm tháng nghiên cứu. Tôi luôn hy vọng rằng, cách giải quyết của tôi về định lý Fermat sẽ truyền cảm hứng cho nhiều người trẻ tuổi yêu toán học và làm việc trên nhiều thách thức cũng như sự hấp hẫn của toán học”.
 Andrew
Wiles đã trải qua gần 8 năm nghiên cứu những bí ẩn trong phương trình
của Fermat đưa ra, cuối cùng bằng cách chứng minh phỏng đoán mô-đun cho
các đường cong eliptic bán ổn định, ông đã giải quyết được một bí ẩn
nhất trong lịch sử toán học. Nghiên cứu của GS Wiles được mô tả mở ra
một thời kỳ mới của lý thuyết số và cho phép các nhà khoa học thúc đẩy
nghiên cứu theo một cách mới.
Andrew
Wiles đã trải qua gần 8 năm nghiên cứu những bí ẩn trong phương trình
của Fermat đưa ra, cuối cùng bằng cách chứng minh phỏng đoán mô-đun cho
các đường cong eliptic bán ổn định, ông đã giải quyết được một bí ẩn
nhất trong lịch sử toán học. Nghiên cứu của GS Wiles được mô tả mở ra
một thời kỳ mới của lý thuyết số và cho phép các nhà khoa học thúc đẩy
nghiên cứu theo một cách mới.
Ngoài nhận danh hiệu Abel, GS Andrew Wiles sẽ nhận được giải thưởng trị giá 710.000 đô la tại lễ trao giải sẽ diễn ra ngày 24/5 tại thủ đô Oslo, Na Uy.
Giải thưởng Abel được sáng lập năm 2001 bởi chính phủ Na Uy, nhằm kỷ niệm 200 năm ngày sinh nhà toán học Na Uy Niels Henrik Abel (1802). Mục đích của giải này là để lấp đi sự thiếu vắng giải Nobel trong toán học, mặc dù huy chương Fields được xem là tương đương. Giải Abel được đi kèm với số tiền thưởng là 6 triệu tiền kroner Na Uy, tương đương với 710.000 đô la.
Giải thưởng này được ví là “Nobel Toán học” của thế giới, danh tiếng tương đương với giải Fields, giải thưởng Toán học danh giá thế giới (mà Giáo sư Ngô Bảo Châu từng vinh dự nhận vào năm 2010 - ND). Là giải thưởng của Viện Khoa học và Văn chương Na Uy, giải Abel sẽ được Na Uy trao hàng năm cho những nhà toán học xuất chúng.
Định lý này phát biểu như sau: “Không tồn tại các nghiệm nguyên khác không x, y, và z thỏa mãn xn + yn = zn trong đó n là một số nguyên lớn hơn”.
Fermat viết lại trên lề một cuốn sách rằng ông có cách giải rất hay, nhưng vì lề sách bé quá không đủ chỗ để viết.
Cho tới đầu thế kỷ 20, các nhà toán học chỉ chứng minh định lý này là đúng với n = 3, 4, 5, 7 và các bội số của nó. Nhà toán học người Đức Ernst Kummer đã chứng minh định lý này là đúng với mọi số nguyên tố tới 100 (trừ 3 số nguyên tố phi chính quy là 37, 59, 67).
Mãi đến những năm 1990, Giáo sư Andrew Wiles cuối cũng đã giải quyết được vấn đề sau 8 năm nghiên cứu. Tháng 8/1995, tại một hội thảo của đại học Boston (Hoa Kỳ), ông đã được giới toán học công nhận công trình nghiên cứu của mình ở tuổi 63.
Trong cuộc trả lời phỏng vấn mới đây với tờ báo The Guardian của Anh, ông nói rằng mình tìm thấy định lý này khi mới 10 tuổi. Ông cho biết: “Giải thưởng là một vinh dự to lớn đối với tôi…. phương trình Fermat là niềm đam mê của tôi từ nhỏ và nó luôn thôi thúc tôi phải hoàn thành trong những năm tháng nghiên cứu. Tôi luôn hy vọng rằng, cách giải quyết của tôi về định lý Fermat sẽ truyền cảm hứng cho nhiều người trẻ tuổi yêu toán học và làm việc trên nhiều thách thức cũng như sự hấp hẫn của toán học”.
Ngoài nhận danh hiệu Abel, GS Andrew Wiles sẽ nhận được giải thưởng trị giá 710.000 đô la tại lễ trao giải sẽ diễn ra ngày 24/5 tại thủ đô Oslo, Na Uy.
Giải thưởng Abel được sáng lập năm 2001 bởi chính phủ Na Uy, nhằm kỷ niệm 200 năm ngày sinh nhà toán học Na Uy Niels Henrik Abel (1802). Mục đích của giải này là để lấp đi sự thiếu vắng giải Nobel trong toán học, mặc dù huy chương Fields được xem là tương đương. Giải Abel được đi kèm với số tiền thưởng là 6 triệu tiền kroner Na Uy, tương đương với 710.000 đô la.
NGUYỄN TÚ (Theo CNN/Wikipedia)
Nguồn: giaoducthoidai.vn
1.1. Fermat và Pascal: Những người đặt nền móng cho lý thuyết xác suất
Blaise Pascal (1623-1662) và Pierre de Fermat (1601-1665) là hai nhà toán học đặt nền tảng cho lý thuyết xác suất hiện đại. Năm 1654, qua trao đổi thư từ, Blaise Pascal và Pierre de Fermat đã giải quyết một bài toán thú vị của lý thuyết trò chơi (Problem of Points) mà ta có thể tóm tắt (link Tiếng Anh) như sau: Vào một ngày nọ, Pascal và Fermat ngồi nói chuyện với nhau trong một quán cà phê ở Paris. Sau một ngày thảo luận căng thẳng về những vấn đề toán học hóc búa, họ quyết định mỗi người sẽ bỏ raVà trong một bức thư gửi Pascal sau này, Fermat đã nêu cách giải quyết như sau:
Tôi (Fermat) chỉ cần
Vì trong
Pascal rất hài lòng với cách giải quyết của Fermat. Tuy nhiên, Pascal nhận thấy phương pháp liệt kê tất cả các trường hợp có thể xảy ra của Fermat tương đối tẻ nhạt đối với bài toán tổng quát. Pascal đã lý luận như sau: Trong lời giải của Fermat, ta nhận thấy nếu có
Đây chính là
Đối với bài toán tổng quát, khi người chơi thứ nhất và người thứ hai lần lượt cần
Trở lại trò chơi của Fermat và Pascal
Cho dù lý luận trên của Fermat và Pascal tương đối đơn giản đối với chúng ta ngày nay, nhưng nó là một cuộc cách mạng vào những năm giữa thế kỷ 17. Đó chính là cách định nghĩa xác suất theo quan điểm cổ điển. Khi một phép thử ngẫu nhiên có
Trong bài toán chia điểm của Fermat và Pascal, có
Bài tập: Hãy trình bày cách chia tiền thưởng trong trường hợp Fermat được
44-Leonard Euler
1707-1783
Thụy Sĩ
Vật Lý, Toán Học
Euler người thầy vĩ đại: Một số đóng góp tiêu biểu
05/05/2016 08:06 -
Trong hai kỳ trước chúng ta đã tìm hiểu cuộc sống
thăng trầm và các đóng góp cơ bản của Euler, kỳ này Tia Sáng giới thiệu
tới bạn đọc một số đóng góp tiêu biểu của Euler, nội dung sẽ bao gồm
nhiều kiến thức Toán học.
Euler với lý thuyết số
Số hoàn hảo
Ngay từ thời của Pythagoras (thế kỷ thứ 6 trước Công nguyên) câu hỏi đặt ra với các số hoàn hảo đã được biết tới.
Định nghĩa số hoàn hảo: Số hoàn hảo là một số nguyên dương mà tổng các ước thực sự của nó bằng chính nó.
Ví dụ: Các ước thực sự của 6 là 1,2,3 và 6=1+2+3.
Trong quá trình nghiên cứu về số hoàn hảo, Euler đã đưa ra một số khái niệm và các khái niệm này đều có những đóng góp to lớn không chỉ cho riêng việc nghiên cứu các số hoàn hảo.
Định nghĩa: σ (n) là tổng các ước nguyên dương của n. (Ban đầu Euler sử dụng kí hiệu ∫(n), ngày nay kí hiệu đó được sử dụng cho tích phân.)
Euler cũng đưa chứng minh nhiều khẳng định liên quan tới σ (n).
Mệnh đề: Nếu n là một số hoàn hảo thì σ (n) = 2n.
Định lý: Nếu n là một số hoàn hảo chẵn thì n = 2k-1 (2k-1) và 2k -1 là một số nguyên tố.
Với định lý nêu trên, Euler đã chỉ ra dạng của các số hoàn hảo chẵn, nhưng như vậy vẫn là chưa đủ cho bộ óc vĩ đại của mình, năm 1747 trong một bài báo của mình, Euler đã đưa ra câu hỏi “Liệu có số hoàn hảo nào là số lẻ?” Sau đó, ông gọi đó là vấn đề khó nhất. Vào thời điểm đó tất cả mọi người đều tin rằng đó là một vấn đề thực sự khó, vì ngay cả Euler cũng xác nhận điều đó.
Cho đến ngày nay, vấn đề về sự tồn tại của một số hoàn hảo lẻ vẫn còn là một thách thức cho tất cả các nhà toán học. Họ vẫn chưa thể khẳng định được sự tồn tại của số hoàn hảo lẻ. Ngay cả với sự trợ giúp của các hệ thống siêu máy tính thì câu hỏi trên vẫn là một câu hỏi mở. Có rất nhiều người đã tham gia nghiên cứu vấn đề này và cũng cho ra nhiều kết quả thú vị.
* Một số hoàn hảo lẻ không thể chia hết cho 105.
* Số hoàn hảo lẻ nhỏ nhất lớn hơn 10300
* Một số hoàn hảo lẻ có ít nhất ba thừa số nguyên tố khác nhau.
* Tổng nghịch đảo của các số hoàn hảo lẻ là hữu hạn.
Đây là một điều rất thú vị bởi trong giải tích thì
Hi vọng trong tương lai gần các nhà Toán học sẽ có câu trả lời cho vấn đề “số hoàn hảo lẻ”.
Số nguyên tố và hàm Zeta
Bắt đầu với bài toán Basel tính tổng nghịch đảo các bình phương
Tổng quát hoá tổng trên ta được hàm Zeta
Euler đã tính được
sau đó Euler viết P(x) dưới 2 dạng khác nhau và đồng nhất hệ số để tính được ζ (2).
Xét hệ số của x2 trong P(x) nói trên, ta có:
Và cuối cùng thu được
Không dừng lại ở đó, Euler còn tính được kết quả tổng quát .
Trong đó |B2n| là số Bernoulli
Euler gặp khó khăn với trường hợp s lẻ và ông không tin nó có liên quan tới
Trong quá trình tính toán với các bài toán trên, Euler đã đưa ra rất nhiều đẳng thức bất ngờ và nhiều điểm độc đáo, sau này trở thành các công cụ tính toán mạnh cho nhiều nhà toán học. Với lý thuyết số, Euler còn chứng minh rất nhiều định lý quan trọng trong lý thuyết đồng dư, số nguyên tố, số Mersenne… do khuôn khổ bài viết nên tôi chỉ trình bày sơ lược các kết quả đại diện trong các lĩnh vực mà Euler để lại.
Euler và định lý cơ bản của đại số
Định lý: Mọi đa thức bậc n với hệ số phức luôn phân tích được thành n nhân tử tuyến tính
Đây là định lý cơ bản của đại số, một trong những định lý quan trọng nhất và được sử dụng rộng rãi không chỉ riêng trong đại số. Các chứng minh của định lý này cho đến nay vẫn chưa có một chứng minh nào là thuần tuý đại số, các chứng minh đã có đều mang chút ít màu sắc của giải tích phức.
Năm 1794, Euler cũng đưa ra một phác thảo chứng minh cho định lý cơ bản của đại số. khi đó Euler mới chỉ cụ thể hoá được trường hợp bậc 4.
Định lý Euler-Fermat và Mật mã
Định lý: Nếu a và n là hai số nguyên tố cùng nhau thì aφ(n) ≡ 1 (mod n). Với φ(n) là phi hàm Euler.
Trong mật mã, ta quan tâm tới việc truyền thông tin một cách an toàn từ người gửi tới người nhận. Một thông điệp M được mã hoá thành E và người nhận sẽ giải mã từ E thu được M. Sẽ rất thuận tiện nếu mỗi kí tự trong bảng mã ASCII được thay thế bằng các số tự nhiên, khi đó việc biến M → E sẽ chuyển sang ngôn ngữ ánh xạ f : N → N. Vấn đề ta phải tìm một hàm f thoả mãn:
- f là một song ánh
- f có công thức và khó tìm được nghịch ảnh của f.
Một giải pháp cho vấn đề này là chương trình mã hóa RSA đang được sử dụng rộng rãi (đặt theo tên nhà phát minh của nó R. Rivet, A. Shamir và Adleman L.)
Tạo Mã và Mã hoá
* Chọn hai số nguyên tố p,q lớn và khác nhau.
* Tính n = p.q
* Tính giá trị của φ(n) = (p-1) (q-1)
* Chọn 1 số nguyên tố e thoả mãn: 1
Mã công khai là n, module và e số mũ công khai, mã bí mật
Người gửi chuyển thông tin M thành số m
Bánh răng Euler
Đĩa Euler
Euler cũng nghiên cứu tới chuyện động của các vật thể xoay quanh một trục, có tính tới ma sát. Một ví dụ thú vị là đĩa Euler, một đĩa tròn (đồng nhất) bằng kim loại được quay trên một bề mặt mịn sạch. Lúc đầu, nó sẽ xoay xung quanh trục thẳng đứng của nó, nhưng do ma sát, trục đang bắt đầu nghiêng và đĩa để cuộn trên một đường tròn. Càng ngày trục nghiêng càng bị nghiêng dần, các vòng tròn thì ngày một rộng ra. Dù có xét đến yếu tố nào đi nữa thì quả bóng vẫn sẽ dừng lại.
Chìa khóa để giải thích chuyển động này là phương trình Euler, một tập hợp các phương trình vi phân liên quan đến các góc Euler và các thông số khác. Các chi tiết kỹ thuật của các chuyển động, vẫn còn được tiếp tục nghiên cứu cho tới tận bây giờ.
Lý thuyết đồ thị và Tôpô
Con sông Pregel, chảy qua thành phố Phổ Königsberg, chia thành phố thành một hòn đảo và ba vùng đất riêng biệt, một ở phía Bắc, một ở phía Đông, và một ở phía Nam. Có tất cả bảy cây cầu, sắp xếp như trong bản đồ với các điểm màu xanh lá cây.
Bài toán: người ta có thể đi dạo từ một điểm ở thành phố khác bằng cách đi qua mỗi cây cầu đúng một lần? Bậc của một đỉnh là cạnh nối với nó; trong đồ thị các cây cầu Königsberg, ba nút có bậc bằng 3 và một nút có bậc 5. Euler đã chứng minh rằng một chu trình có dạng như mong muốn chỉ tồn tại khi và chỉ khi không có nút bậc lẻ. Một đường đi như vậy được gọi là một chu trình Euler. Do đồ thị các cây cầu Königsberg có bốn nút bậc lẻ, nên nó không thể có chu trình Euler.
Lời giải của Euler cho bài toán trên là cơ sở cho nền móng của Topo học. (Xem thêm bài viết của Nguyễn Hữu Việt Hưng trên Tia Sáng số 6 - 20/3/2016.)
Công thức Euler
Với mọi số thực x ta luôn có: eix = cos x + i.sin x . Với e là số vô tỉ được tính qua giới hạn
công thức Euler là phổ biến trong toán học, vật lý và kỹ thuật. Nhà vật lý Richard Feynman được gọi là phương trình “viên ngọc quý” và “công thức đáng chú ý nhất trong toán học.”
Một công thức tương đương là ix= ln (cos x + i sin x), công thức này được đưa ra bởi Cotes (1714). Công thức Euler được sử dụng trong rất nhiều lĩnh vực của Toán từ lý thuyết số phức, phương trình vi phân,…từ đơn giản nhất cho đến phức tạp.
Qua ba bài viết, chúng ta đã cùng có một hành trình xuyên suốt cuộc đời và sự nghiệp của nhà Toán học vĩ đại Euler, một người thầy vĩ đại bởi tất cả những gì ông để lại đã trực tiếp hoặc gián tiếp tạo nên bộ mặt khoa học và cuộc sống ngày nay.
Leonhard Euler - Sức mạnh trí tuệ kỳ diệu
Ngày 18/9/1783, nhà
toán học, nhà vật lý học Leonhard Euler - người có một sức mạnh trí tuệ
và tinh thần kỳ diệu, đã rời bỏ khoa học để đi về thế giới bên kia.
Song những gì ông để lại vẫn luôn được hậu thế nâng niu và trân trọng
không chỉ vì giá trị thực tế của nó mà còn bởi giá trị tinh thần to lớn
ẩn chứa bên trong.
Ngay từ nhỏ Euler
là một cậu bé có tài năng đặc biệt về ngôn ngữ và một trí nhớ phi
thường. Song cuộc đời ông đã trải qua nhiều biến động và bất hạnh: hai
mắt lần lượt hỏng, nhà cháy thiêu rụi mọi tài sản, người vợ thân yêu qua
đời...

Leonhard Euler sinh ngày 15/4/1707 tại Basel, Thụy Sĩ.
|
Nhưng tất cả những điều đó không hề ảnh hưởng tới sức sáng tạo, đến khả năng làm việc của ông. Càng về già, Euler càng làm việc không biết mệt mỏi. Chỉ tính riêng trong 17 năm cuối đời, Euler đã
công bố tới 416 công trình. Tính ra trung bình mỗi năm ông công bố tới
25 công trình, nhiều gấp 3 lần số công trình mỗi năm trước đó ông đã
công bố.
Sau khi ông qua đời, các công trình
nghiên cứu của ông đã được tập hợp trong bộ sách “Leonhard Euler Opera
Omnia”, gồm 85 quyển cỡ lớn với gần 40.000 trang, trong đó đề cập đến
hầu hết các lĩnh vực của toán học và nhiều ngành khoa học kỹ thuật khác.
Đóng góp quan trọng cho Toán học
Đối với Euler,
làm toán cũng tự nhiên và cần thiết cho đời sống như là hít thở khí
trời vậy. Ông đã bị ám ảnh bởi sự biến đổi kỳ diệu của những phép tính
cho đến tận khi ông qua đời. Leonhard Euler
nghiên cứu hầu hết các lĩnh vực của Toán học thời bấy giờ như: đại số,
lý thuyết số, giải tích, hình học… Các công trình về toán học chiếm tới
58% tổng các công trình nghiên cứu của ông.
Một trong những thành công ban đầu của Euler
đã là tìm ra lời giải cho bài toán Basel, yêu cầu tìm giá trị chính xác
của tổng các bình phương nghịch đảo của các các số nguyên. Trước đó,
các nhà toán học tốn rất nhiều công sức mà không tìm ra được kết quả bài
toán. Đến năm 1735, khi Euler sử dụng kỹ thuật tính xấp xỉ mới tìm ra kết quả chính xác của bài toán là pi^2/16.
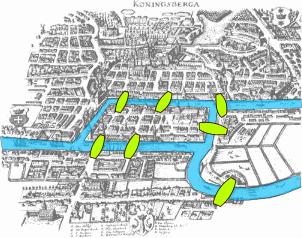
Bản đồ Königsberg thời Euler, mô tả vị trí thực của 7 cây cầu và sông Pregel.
|
Năm 1736, Euler tiếp tục giải được bài toán nổi tiếng 7 chiếc cầu Königsberg.
Khi đó, thành phố Königsberg gồm hai hòn đảo nối với nhau và với đất
liền bởi 7 cây cầu. Bài toán đặt ra là tìm một tuyến đường đi qua mỗi
cây cầu chỉ đúng 1 lần. Bằng lý thuyết đồ thị, Euler đã
chứng minh rằng điều đó không thể thực hiện. Lời giải của ông cho bài
toán này được coi là định lý đầu tiên của lý thuyết đồ thị và là đánh
dấu sự phát triển của ngành tôpô học.
Không dừng lại ở thành công đó, Euler
tiếp tục nghiên cứu và công bố nhiều công trình toán học quan trọng
khác như: chuyển động cơ học được giải thích bởi ngành giải tích, đường
thẳng Euler, đường tròn Euler trong tam giác, định lý Euler về
liên hệ giữa số đỉnh, cạnh và mặt trong của một đa diện lồi, nhập môn
về tính vi tích, nguyên lý vi phân học, nguyên lý tích phân học, dẫn
luận phân tích vô cùng nhỏ, … Ngoài ra, Euler còn phát minh ra một chuỗi các phương pháp tính xấp xỉ, được sử dụng nhiều trong tính toán.
Ông
cũng là người đưa ra nhiều kí hiệu toán học mà ngày nay chúng ta vẫn
đang sử dụng như: số "pi" để biểu diễn tỉ lệ giữa chu vi đường tròn và
đường kính của nó, sin, cos, tg, cotg, Δx (số gia), Σ (tổng), f(x) (hàm f
của x), v.v...
Đóng góp cho vật lý và các ngành khoa học kỹ thuật
Euler
có nhiều đóng góp cho cơ học, vật lý. Ông đặc biệt nghiên cứu các định
luật chuyển động của Issac Newton. Quá trình nghiên cứu này đã giúp ông
giải thích các định luật vật lý học Newton dưới dạng toán giải tích,
đồng thời giúp ông phát hiện ra nhiều lý thuyết vật lý khác. Ví dụ khi Euler chứng minh được qui luật vận động của các chất lỏng mà Issac Newton đã đưa ra, Leonhard Euler đã phát triển được lý thuyết về sự cân bằng thủy lực.
Tương tự như thế, thông qua việc phân tích sự vận động của thể rắn và áp dụng các định luật của Newton, Euler
đã giải thích được một cách cặn kẽ về quá trình biến dạng của các vật
thể rắn khi có sự tác động của các lực bên ngoài, từ đó góp phần hình
thành lý thuyết đàn hồi. Năm 1936, các công trình nghiên cứu này của ông
đã được tập hợp trong luận văn “Lực học”.

Chân dung Leonhard Euler trên một con tem của Thụy Sĩ.
|
Ngoài vật lý, Euler cũng
nghiên cứu về thiên văn học, lý thuyết đường đạn, bản đồ, xây dựng, lý
thuyết âm nhạc, thần học và triết học,… Trong những năm tháng mù lòa,
ông đã viết một luận án dài 775 trang về chuyển động của mặt trăng. Ông
cũng nghiên cứu về quỹ đạo của sao Thiên Vương, nhờ đó các nhà thiên văn
học tìm ra sao Hải Vương sau này.
Với những đóng góp cho khoa học, Euler
được phong làm viện sỹ của 8 viện hàn lâm trên thế giới, trong đó có
Anh, Pháp, Nga, Đức,…Ông cũng được coi là nhà toán học quan trọng nhất
của thế kỷ XVIII.
Đánh giá về những công trình khoa học của Euler,
nhà triết học duy vật nổi tiếng người Pháp Diderot đã viết: “Ông sẵn
sàng đánh đổi tất cả những điều ông đã xây dựng được để lấy một trang
trong những tác phẩm của ngài Euler".
Trung tâm Thông tin Tư liệu/TTXVN
Leonard Euler - Nhà toán học vĩ đại của nhân loại
Ngày đăng: 2014-04-26
BBT
xin giới thiệu với các bạn bài viết mở đầu trong loạt bài viết về
Leonhard Euler, được bạn madness trích đoạn và dịch từ quyển sách Euler –
The master of us all của tác giả William Dunhamm, bài viết này giới
thiệu qua về tiểu sử và cuộc đời của Euler – nhà toán học thiên tài thế
kỷ XVIII.
Cuộc
đời của Euler (1707-1783) được gói gọn trong thế kỉ 18: 76 năm từ mùa
xuân 1707 tới mùa thu năm 1783. Cùng thời với ông còn có rất nhiều tên
tuổi nổi tiếng: Benjamin Franklin (1706-1790), Washington (1732-1799),
Robespierre (1758-1794), Captain Cook (1728-1779). Leonhard Euler được
sinh ra tại Basel, Thụy Sĩ. Cha ông là một giáo sĩ Tin Lành và luôn hy
vọng Leonhard sẽ theo bước ông trên những bục giảng kinh. Mẹ ông cũng
xuất thân từ một gia đình mục sư, vì thế chàng trai trẻ Euler dường như
được sinh ra để dành cho tôn giáo.
Thuở nhỏ, Euler là cậu bé được ban tặng một tài năng đặc biệt về ngôn ngữ và một trí nhớ phi thường. Cậu còn có khả năng thực hiện những phép tính phức tạp mà không cần giấy bút. Năm 14 tuổi, Euler vào trường Đại học Basel dưới sự dẫn dắt của một giáo sư Toán nổi tiếng: Johann Bernoulli (1667-1748).
Từ năm 1721, Bernoulli được xem như là nhà toán học giỏi nhất thời bấy giờ (Leibniz đã mất vài năm trước, Newton đã từ bỏ Toán học vì tuổi tác). Bernoulli – một người rất ít khi khen ngợi người khác – đã từng viết cho Euler: “Tôi trình bày các phép tích phân như một sự khởi đầu, nhưng chính cậu là người đã đưa nó đến sự trưởng thành.” Tại Đại học, Euler không chỉ học Toán mà còn phải học Thần học, viết về Lịch Sử của Luật và hoàn tất bằng Thạc sỹ về Triết học. Nhưng vì lòng đam mê Toán học, ông đã quyết định rời bỏ khoa Thần học và trở thành một nhà toán học.
Năm 20 tuổi, Euler trở nên nổi tiếng qua các kì thi khoa học quốc tế. Năm 1727, Euler tới học viện St. Petersburg theo lời mời của Daniel Bernoulli (1700-1782) (con trai của Johann Bernoulli), và tham gia cùng Daniel trong các cuộc thảo luận về Vật lý và Toán học. Vào năm 1733, Daniel rời khỏi học viện và để lại một vị trí quan trọng mà không lâu sau Euler được bổ nhiệm vào. Không lâu sau, Euler cưới Kathariana Gsell – con gái một họa sỹ và sau hơn bốn mươi năm chung sống, 13 “Euler con” đã chào đời.
Một trong những thành công ban đầu của Euler là lời giải cho bài toán Basel – một vấn đề hóc búa đã làm đau đầu các nhà toán học của thế kỉ trước. Năm 1644, bài toán Basel được đưa ra bởi Pietro Mengoli (1625-1686) với yêu cầu tìm ra giá trị chính xác của tổng:(1+14+19+...+1k2+...) . Những kết quả xấp xỉ cho thấy tổng trên gần bằng 85 .
Tuy nhiên, kết quả chính xác vẫn nằm trong “vùng tối” cho tới năm 1735,
Euler đưa ra đáp án gây ngạc nhiên cho các nhà toán học: π26 .
Tiếp theo đó, các bài báo của ông (papers) cứ lần lượt được xuất bản
thông qua tạp chí khoa học của học viện St. Petersburg. Trong một số ấn
phẩm, một nửa các bài báo xuất bản thuộc về Euler.
Thời gian Euler ở St. Petersburg sẽ là một cuộc sống trong thiên đường Toán học nếu như ông không gặp phải một số khó khăn khá lớn. Thứ nhất, sự rối loạn chính trị trong nước Nga sau cái chết bất ngờ của Catherine I đã gây nên một sự xôn xao trong giới học viện về vị trí của Euler khi Học viện này chỉ có các nhà khoa học người Nga. Tiếp theo đó là sự không thoải mái của Euler khi Học viện được điều hành bởi một quan chức luôn tìm cách kiềm chế tài năng khoa học. Vấn đề thứ ba là sự suy giảm thị lực nghiêm trọng của Euler: năm 1738 (31 tuổi) ông đã bị mù mắt bên phải, tuy nhiên ông đã không để điều này làm ảnh hưởng tới các hoạt động nghiên cứu của mình. Ông tiếp tục viết các bài báo về thiết kế tàu, âm học, và lý thuyết về hòa âm. Được sự động viên của bạn ông – Christian Golbach (1690-1764), Euler đã đưa ra các kết quả trong Lý thuyết số, và Số học Giải tích, và đặt nền móng cho Toán Tổ hợp. Trong thời gian này, Euler đã viết tác phẩm Mechanica trình bày các định luật chuyển động của Newton dưới dạng Toán giải tích. Do đó Mechanica được đánh giá là một bước ngoặt lớn trong lịch sử Vật lý. Với những thành quả như thế, tiếng tăm của Euler đã khiến Hoàng đế nước Phổ -Frederick Đại Đế – (1712-1786) mời ông vào Học viện Berlin.
Bởi vì tình hình chính trị bất ổn ở Nga (mà Euler đã miêu tả rằng: “một đất nước nơi mỗi người phát biểu ý kiến đều bị treo cổ”), Euler đã cùng gia đình chuyển sang Đức vào năm 1741. Trong thời gian ở Đức, Euler đã xuất bản 2 tác phẩm nổi tiếng nhất của ông: Introductio in analysin infinitorum (1748) và Institutiones calcul differentialis (1755), với khám phá ra số phức, đẳng thức Euler:eia=cosa+isina , và một chứng minh cho định lý cơ bản của đại số.
Tại Berlin, Euler đã được mời giảng thuyết các vấn đề khoa học phổ thông cho Quận chúa Anhalt Dessau. Kết quả là một tác phẩm lớn bao gồm nhiều tập, liên tục được xuất bản dưới dạng những lá thư giảng giải cho Quận chúa: Những bức thư gửi Quận chúa (Letters of Euler of Different Subjects in Natural Philosophy Addressed to a German Princess). Tuyển tập này bao gồm hơn 200 “lá thư” giới thiệu các chủ đề rất đa dạng như ánh sáng, âm thanh, trọng lực, logic, ngôn ngữ, từ trường, và thiên văn học. Những bức thư gửi Quận chúa ngay lập tức trở nên nổi tiếng và được dịch ra rất nhiều ngôn ngữ, cuối cùng nó đã trở thành tác phẩm được đọc nhiều nhất của Euler.
Mặc dù đã xa nước Nga, từ Đức Euler vẫn tiếp tục làm chủ bút cho tạp chí khoa học của St. Petersburg và xuất bản nhiều bài báo cho tạp chí. Bên cạnh những nghiên cứu toán học, ông còn đảm trách nhiều nhiệm vụ về quản lý tại Học viện Berlin như một người quản lý (không chính thức). Tuy nhiên, Frederick Đại đế là một người tự cao và coi khinh những học giả lớn thời bấy giờ; thêm vào đó là sự bất hòa giữa ông và Voltaire tại Học viện Berlin. Những điều này đã khiến Euler bị mất vị trí tại Học viện, sau đó ông quyết định trở lại Học viện St. Petersburg do tình hình chính trị tại Nga đã có những chuyển biến tốt đẹp.
Mặc dù sự nghiên cứu khoa học của ông đạt những thành quả rất tốt đẹp, trong một vài năm ông đã gặp 2 biến cố bất hạnh. Năm 1771, ông đã bị mù hoàn toàn khi con mắt còn lại cũng không thể được cứu chữa. 2 năm sau, Katharina qua đời. Những biến cố này đã báo hiệu dấu chấm hết cho những năm nghiên cứu miệt mài của ông. Tuy nhiên, Euler vẫn tiếp tục xuất bản một bài báo một tuần. Trong những năm tháng mù lòa, ông đã viết một quyển sách về đại số, một luận án dài 775 trang về chuyển động của mặt trăng, và 3 tập sách dày phát triển những kết quả về tích phân. Những năm cuối đời ông đã đưa ra các nghiên cứu quan trọng về thiên văn học như hoạt động của sao Thiên Vương, những phương trình về quỹ đạo giúp các nhà thiên văn học tìm ra sao Hải Vương.
Năm 1783, trong một buổi chiều thứ bảy bận rộn như mọi ngày, Euler đã qua đời trong một cơn xuất huyết. Gia đình, đồng nghiệp, Học viện, và cả cộng đồng khoa học an táng thi hài ông tại St. Petersburg và thương tiếc đưa tiễn ông về nơi an nghỉ cuối cùng.
Thuở nhỏ, Euler là cậu bé được ban tặng một tài năng đặc biệt về ngôn ngữ và một trí nhớ phi thường. Cậu còn có khả năng thực hiện những phép tính phức tạp mà không cần giấy bút. Năm 14 tuổi, Euler vào trường Đại học Basel dưới sự dẫn dắt của một giáo sư Toán nổi tiếng: Johann Bernoulli (1667-1748).
Từ năm 1721, Bernoulli được xem như là nhà toán học giỏi nhất thời bấy giờ (Leibniz đã mất vài năm trước, Newton đã từ bỏ Toán học vì tuổi tác). Bernoulli – một người rất ít khi khen ngợi người khác – đã từng viết cho Euler: “Tôi trình bày các phép tích phân như một sự khởi đầu, nhưng chính cậu là người đã đưa nó đến sự trưởng thành.” Tại Đại học, Euler không chỉ học Toán mà còn phải học Thần học, viết về Lịch Sử của Luật và hoàn tất bằng Thạc sỹ về Triết học. Nhưng vì lòng đam mê Toán học, ông đã quyết định rời bỏ khoa Thần học và trở thành một nhà toán học.
Năm 20 tuổi, Euler trở nên nổi tiếng qua các kì thi khoa học quốc tế. Năm 1727, Euler tới học viện St. Petersburg theo lời mời của Daniel Bernoulli (1700-1782) (con trai của Johann Bernoulli), và tham gia cùng Daniel trong các cuộc thảo luận về Vật lý và Toán học. Vào năm 1733, Daniel rời khỏi học viện và để lại một vị trí quan trọng mà không lâu sau Euler được bổ nhiệm vào. Không lâu sau, Euler cưới Kathariana Gsell – con gái một họa sỹ và sau hơn bốn mươi năm chung sống, 13 “Euler con” đã chào đời.
Một trong những thành công ban đầu của Euler là lời giải cho bài toán Basel – một vấn đề hóc búa đã làm đau đầu các nhà toán học của thế kỉ trước. Năm 1644, bài toán Basel được đưa ra bởi Pietro Mengoli (1625-1686) với yêu cầu tìm ra giá trị chính xác của tổng:
Thời gian Euler ở St. Petersburg sẽ là một cuộc sống trong thiên đường Toán học nếu như ông không gặp phải một số khó khăn khá lớn. Thứ nhất, sự rối loạn chính trị trong nước Nga sau cái chết bất ngờ của Catherine I đã gây nên một sự xôn xao trong giới học viện về vị trí của Euler khi Học viện này chỉ có các nhà khoa học người Nga. Tiếp theo đó là sự không thoải mái của Euler khi Học viện được điều hành bởi một quan chức luôn tìm cách kiềm chế tài năng khoa học. Vấn đề thứ ba là sự suy giảm thị lực nghiêm trọng của Euler: năm 1738 (31 tuổi) ông đã bị mù mắt bên phải, tuy nhiên ông đã không để điều này làm ảnh hưởng tới các hoạt động nghiên cứu của mình. Ông tiếp tục viết các bài báo về thiết kế tàu, âm học, và lý thuyết về hòa âm. Được sự động viên của bạn ông – Christian Golbach (1690-1764), Euler đã đưa ra các kết quả trong Lý thuyết số, và Số học Giải tích, và đặt nền móng cho Toán Tổ hợp. Trong thời gian này, Euler đã viết tác phẩm Mechanica trình bày các định luật chuyển động của Newton dưới dạng Toán giải tích. Do đó Mechanica được đánh giá là một bước ngoặt lớn trong lịch sử Vật lý. Với những thành quả như thế, tiếng tăm của Euler đã khiến Hoàng đế nước Phổ -Frederick Đại Đế – (1712-1786) mời ông vào Học viện Berlin.
Bởi vì tình hình chính trị bất ổn ở Nga (mà Euler đã miêu tả rằng: “một đất nước nơi mỗi người phát biểu ý kiến đều bị treo cổ”), Euler đã cùng gia đình chuyển sang Đức vào năm 1741. Trong thời gian ở Đức, Euler đã xuất bản 2 tác phẩm nổi tiếng nhất của ông: Introductio in analysin infinitorum (1748) và Institutiones calcul differentialis (1755), với khám phá ra số phức, đẳng thức Euler:
Tại Berlin, Euler đã được mời giảng thuyết các vấn đề khoa học phổ thông cho Quận chúa Anhalt Dessau. Kết quả là một tác phẩm lớn bao gồm nhiều tập, liên tục được xuất bản dưới dạng những lá thư giảng giải cho Quận chúa: Những bức thư gửi Quận chúa (Letters of Euler of Different Subjects in Natural Philosophy Addressed to a German Princess). Tuyển tập này bao gồm hơn 200 “lá thư” giới thiệu các chủ đề rất đa dạng như ánh sáng, âm thanh, trọng lực, logic, ngôn ngữ, từ trường, và thiên văn học. Những bức thư gửi Quận chúa ngay lập tức trở nên nổi tiếng và được dịch ra rất nhiều ngôn ngữ, cuối cùng nó đã trở thành tác phẩm được đọc nhiều nhất của Euler.
Mặc dù đã xa nước Nga, từ Đức Euler vẫn tiếp tục làm chủ bút cho tạp chí khoa học của St. Petersburg và xuất bản nhiều bài báo cho tạp chí. Bên cạnh những nghiên cứu toán học, ông còn đảm trách nhiều nhiệm vụ về quản lý tại Học viện Berlin như một người quản lý (không chính thức). Tuy nhiên, Frederick Đại đế là một người tự cao và coi khinh những học giả lớn thời bấy giờ; thêm vào đó là sự bất hòa giữa ông và Voltaire tại Học viện Berlin. Những điều này đã khiến Euler bị mất vị trí tại Học viện, sau đó ông quyết định trở lại Học viện St. Petersburg do tình hình chính trị tại Nga đã có những chuyển biến tốt đẹp.
Mặc dù sự nghiên cứu khoa học của ông đạt những thành quả rất tốt đẹp, trong một vài năm ông đã gặp 2 biến cố bất hạnh. Năm 1771, ông đã bị mù hoàn toàn khi con mắt còn lại cũng không thể được cứu chữa. 2 năm sau, Katharina qua đời. Những biến cố này đã báo hiệu dấu chấm hết cho những năm nghiên cứu miệt mài của ông. Tuy nhiên, Euler vẫn tiếp tục xuất bản một bài báo một tuần. Trong những năm tháng mù lòa, ông đã viết một quyển sách về đại số, một luận án dài 775 trang về chuyển động của mặt trăng, và 3 tập sách dày phát triển những kết quả về tích phân. Những năm cuối đời ông đã đưa ra các nghiên cứu quan trọng về thiên văn học như hoạt động của sao Thiên Vương, những phương trình về quỹ đạo giúp các nhà thiên văn học tìm ra sao Hải Vương.
Năm 1783, trong một buổi chiều thứ bảy bận rộn như mọi ngày, Euler đã qua đời trong một cơn xuất huyết. Gia đình, đồng nghiệp, Học viện, và cả cộng đồng khoa học an táng thi hài ông tại St. Petersburg và thương tiếc đưa tiễn ông về nơi an nghỉ cuối cùng.
Theo SysNet Wiki
Đồ thị Euler
Đường đi Euler
[CÂU CHUYỆN TOÁN HỌC] - BÀI TOÁN BẢY CÂY CẦU CỦA KONIGSBERG
Câu chuyện bắt đầu vào thế kỉ 18, tại thị trấn Konigsberg yên bình của nước Phổ, bên bờ sông Pregel. Năm 1254, các hiệp sĩ Teuton thành lập thành phố Konigsberg dưới sự trị vì của vị vua Bohemian Ottoker II sau cuộc chinh chiến thứ hai trước người Phổ. Thời Trung Đại, Konigsberg trở thành thành phố trọng điểm và là trung tâm giao dịch với vị trí đắc địa bên bờ sông. Các bức họa của thế kỉ 18 cho thấy Konigsberg là thành phố phồn thịnh, với hàng trăm tàu cập bến trải sông Pregel với những thương vụ mang lại lợi ích cho người dân địa phương và gia đình của họ. Nền kinh tế ổn định này giúp thành phố xây dựng bảy cây cầu, phần lớn nối với đảo Kneiphof, như hình bên dưới.
Với dòng sông chảy bao quanh Kneiphof, và một hòn đảo khác, nó chia thành phố thành 4 vùng. Theo kể lại, người dân thường dành ngày Chủ Nhật dạo quanh thành phố xinh đẹp này. Lúc này, họ nảy ra một ý tưởng, một trò chơi để tìm ra câu trả lời cho câu hỏi:
“Có đường đi nào cho phép một người đi qua cả bảy cây cầu, mà mỗi cây cầu chỉ đi qua một lần?”
Kết quả là không ai có thể làm được điều này và họ cũng không chứng minh được rằng điều đó là không khả thi. May mắn thay, thị trấn của họ không xa St. Petersburg, nơi có nhà toán học thiên tài Leonard Euler.
Tại sao Euler lại quan tâm đến một vấn đề hoàn toàn không liên quan gì tới toán học? Tại sao nhà toán học thiên tài này lại dành nhiều thời gian cho một vấn đề nhỏ nhặt như thế này? Ban đầu, Euler đã từ chối vì nghĩ rằng nó chẳng liên quan gì đến toán học cả, theo như bức thư phản hồi đề nghị giải quyết của Carl Leohard Gottlieb Ehler năm 1736:
“… Thưa ngày, lời giải cho vấn đề này không liên quan đến toán học và tôi cũng không hiểu tại sao ngài lại mong một nhà toán học giải quyết nó, khi mà lời giải có thể dựa vào lý luận mà không phụ thuộc bất kì nguyên tắc toán học nào.”
Tuy thế, Euler vẫn cảm thấy hứng thú về nó. Trong một lá thư gửi cùng năm cho Giovanni Marioni, một nhà toán học và kỹ sư người Ý, Euler nói:
“Vấn đề này thật nhàm chán, nhưng tôi cho rằng đáng được để tâm vì cả hình học, lẫn đại số, lẫn phương pháp đếm đều chưa đủ để giải quyết nó.”
Euler tin rằng vấn đề này liên quan đến một chủ để mà Gottfried Wilhelm Leibniz từng bàn luận và mong mỏi được nghiên cứu cùng, gọi là geometria situs, hay hình học của vị trí. Đó là tiền thân của lý thuyết đồ thị, một mảng toán học được quan tâm nghiên cứu rất nhiều hiện nay.
Để giải quyết bài toán, đầu tiên, Euler nhận định rằng đường đi cụ thể là không quan trọng và có thể giản lược thành 4 điểm, gọi là các đỉnh, với các đoạn thẳng nối chung tượng trưng cho các cây cầu, gọi là các cạnh. Đồ thị này cho phép ta tính toán bậc của các đỉnh, hay số cạnh nối với nó.
Để ý rằng, khi đi qua một vùng, người đi phải qua một cây cầu rồi rời đi qua một câu cầu khác. Do đó, luôn tồn tại một cặp cạnh đến và đi và vì vậy mà bậc của một đỉnh luôn là số chẵn, chỉ trừ khi đó là điểm bắt đầu và điểm kết thúc.
Trong bài toán bảy câu cầu, để ý rằng tất cả đỉnh đều có bậc lẻ và do đó sẽ luôn có một cây cầu phải đi qua hai lần, bất kể đi thế nào.
Euler cũng tìm ra kết quả tổng quát cho các đồ thị có nhiều hơn hai đỉnh. Một đường đi qua tất cả các cạnh và mỗi cạnh chỉ đi qua một lần được gọi là đường đi Euler, và chỉ tồn tại khi đồ thị thỏa mãn:
1/ Chỉ tồn tại hai đỉnh có bậc lẻ là hai đỉnh bắt đầu và kết thúc, các đỉnh còn lại có bậc chẵn
2/ Tất cả các đỉnh đều có bậc chẵn, đường đi này có điểm đầu và điểm cuối trùng nhau và được gọi là chu trình Euler
Euler cũng chỉ ra một cách để tạo đường đi Euler cho bài toán này là bỏ đi một cây cầu trong số bảy cây. Trên thực tế, lịch sử đã làm chuyện này và số phận của thành phố Konigsberg không được huy hoàng như bài toán đặt tên theo nó.
Năm 1875, người dân Konigsberg quyết định ây một cây cầu mới nối hai bờ sông, tăng bậc của hai đỉnh này lên 4 và do đó chỉ còn hai đỉnh có bậc lẻ, vấn đề đã được giải quyết. Tuy nhiên, có lẽ việc xây dựng cây cầu không liên quan đến mong muốn giải quyết bài toán nổi tiếng này. Năm 1944, chỉ 4 ngày trong tháng tám, quân đội Anh đã đánh bom thành phố này. Đầu năm 1945, khu vực xung quanh Konigsberg bị vây quanh bởi quân đội Nga. Người Đức bắt đầu di tản nhưng quá muộn, hàng ngàn người chết khi cố gắng vượt qua dòng sông băng giá. Tháng 4/1945, Hồng Quân chiếm lĩnh Konigsberg khi nó chỉ còn là đống tro tàn.
Cho tới nay, thị trấn đã trải qua nhiều thay đổi. Phần lớn cây cầu đã bị phá hủy trong cuộc đánh bom và bài toán nổi tiếng thời ấy trở nên không tồn tại. Thị trấn được đổi tên thành Kaliningrad và sống Pregal trở thành Pregolya. Tuy không còn Konigsberg sẽ luôn được ghi nhận là nơi đã hình thành nên một hướng đi hoàn toàn mới của toán học: lý thuyết đồ thị.
Tham khảo:
+ Leonard Euler's Solution to the Konigsberg Bridge Problem, Teo Paoletti http://www.maa.org/…/leonard-eulers-solution-to-the-konigsb…
+ How the Königsberg bridge problem changed mathematics, Dan Van der Vieren https://www.youtube.com/watch?v=nZwSo4vfw6c
Câu chuyện bắt đầu vào thế kỉ 18, tại thị trấn Konigsberg yên bình của nước Phổ, bên bờ sông Pregel. Năm 1254, các hiệp sĩ Teuton thành lập thành phố Konigsberg dưới sự trị vì của vị vua Bohemian Ottoker II sau cuộc chinh chiến thứ hai trước người Phổ. Thời Trung Đại, Konigsberg trở thành thành phố trọng điểm và là trung tâm giao dịch với vị trí đắc địa bên bờ sông. Các bức họa của thế kỉ 18 cho thấy Konigsberg là thành phố phồn thịnh, với hàng trăm tàu cập bến trải sông Pregel với những thương vụ mang lại lợi ích cho người dân địa phương và gia đình của họ. Nền kinh tế ổn định này giúp thành phố xây dựng bảy cây cầu, phần lớn nối với đảo Kneiphof, như hình bên dưới.
Với dòng sông chảy bao quanh Kneiphof, và một hòn đảo khác, nó chia thành phố thành 4 vùng. Theo kể lại, người dân thường dành ngày Chủ Nhật dạo quanh thành phố xinh đẹp này. Lúc này, họ nảy ra một ý tưởng, một trò chơi để tìm ra câu trả lời cho câu hỏi:
“Có đường đi nào cho phép một người đi qua cả bảy cây cầu, mà mỗi cây cầu chỉ đi qua một lần?”
Kết quả là không ai có thể làm được điều này và họ cũng không chứng minh được rằng điều đó là không khả thi. May mắn thay, thị trấn của họ không xa St. Petersburg, nơi có nhà toán học thiên tài Leonard Euler.
Tại sao Euler lại quan tâm đến một vấn đề hoàn toàn không liên quan gì tới toán học? Tại sao nhà toán học thiên tài này lại dành nhiều thời gian cho một vấn đề nhỏ nhặt như thế này? Ban đầu, Euler đã từ chối vì nghĩ rằng nó chẳng liên quan gì đến toán học cả, theo như bức thư phản hồi đề nghị giải quyết của Carl Leohard Gottlieb Ehler năm 1736:
“… Thưa ngày, lời giải cho vấn đề này không liên quan đến toán học và tôi cũng không hiểu tại sao ngài lại mong một nhà toán học giải quyết nó, khi mà lời giải có thể dựa vào lý luận mà không phụ thuộc bất kì nguyên tắc toán học nào.”
Tuy thế, Euler vẫn cảm thấy hứng thú về nó. Trong một lá thư gửi cùng năm cho Giovanni Marioni, một nhà toán học và kỹ sư người Ý, Euler nói:
“Vấn đề này thật nhàm chán, nhưng tôi cho rằng đáng được để tâm vì cả hình học, lẫn đại số, lẫn phương pháp đếm đều chưa đủ để giải quyết nó.”
Euler tin rằng vấn đề này liên quan đến một chủ để mà Gottfried Wilhelm Leibniz từng bàn luận và mong mỏi được nghiên cứu cùng, gọi là geometria situs, hay hình học của vị trí. Đó là tiền thân của lý thuyết đồ thị, một mảng toán học được quan tâm nghiên cứu rất nhiều hiện nay.
Để giải quyết bài toán, đầu tiên, Euler nhận định rằng đường đi cụ thể là không quan trọng và có thể giản lược thành 4 điểm, gọi là các đỉnh, với các đoạn thẳng nối chung tượng trưng cho các cây cầu, gọi là các cạnh. Đồ thị này cho phép ta tính toán bậc của các đỉnh, hay số cạnh nối với nó.
Để ý rằng, khi đi qua một vùng, người đi phải qua một cây cầu rồi rời đi qua một câu cầu khác. Do đó, luôn tồn tại một cặp cạnh đến và đi và vì vậy mà bậc của một đỉnh luôn là số chẵn, chỉ trừ khi đó là điểm bắt đầu và điểm kết thúc.
Trong bài toán bảy câu cầu, để ý rằng tất cả đỉnh đều có bậc lẻ và do đó sẽ luôn có một cây cầu phải đi qua hai lần, bất kể đi thế nào.
Euler cũng tìm ra kết quả tổng quát cho các đồ thị có nhiều hơn hai đỉnh. Một đường đi qua tất cả các cạnh và mỗi cạnh chỉ đi qua một lần được gọi là đường đi Euler, và chỉ tồn tại khi đồ thị thỏa mãn:
1/ Chỉ tồn tại hai đỉnh có bậc lẻ là hai đỉnh bắt đầu và kết thúc, các đỉnh còn lại có bậc chẵn
2/ Tất cả các đỉnh đều có bậc chẵn, đường đi này có điểm đầu và điểm cuối trùng nhau và được gọi là chu trình Euler
Euler cũng chỉ ra một cách để tạo đường đi Euler cho bài toán này là bỏ đi một cây cầu trong số bảy cây. Trên thực tế, lịch sử đã làm chuyện này và số phận của thành phố Konigsberg không được huy hoàng như bài toán đặt tên theo nó.
Năm 1875, người dân Konigsberg quyết định ây một cây cầu mới nối hai bờ sông, tăng bậc của hai đỉnh này lên 4 và do đó chỉ còn hai đỉnh có bậc lẻ, vấn đề đã được giải quyết. Tuy nhiên, có lẽ việc xây dựng cây cầu không liên quan đến mong muốn giải quyết bài toán nổi tiếng này. Năm 1944, chỉ 4 ngày trong tháng tám, quân đội Anh đã đánh bom thành phố này. Đầu năm 1945, khu vực xung quanh Konigsberg bị vây quanh bởi quân đội Nga. Người Đức bắt đầu di tản nhưng quá muộn, hàng ngàn người chết khi cố gắng vượt qua dòng sông băng giá. Tháng 4/1945, Hồng Quân chiếm lĩnh Konigsberg khi nó chỉ còn là đống tro tàn.
Cho tới nay, thị trấn đã trải qua nhiều thay đổi. Phần lớn cây cầu đã bị phá hủy trong cuộc đánh bom và bài toán nổi tiếng thời ấy trở nên không tồn tại. Thị trấn được đổi tên thành Kaliningrad và sống Pregal trở thành Pregolya. Tuy không còn Konigsberg sẽ luôn được ghi nhận là nơi đã hình thành nên một hướng đi hoàn toàn mới của toán học: lý thuyết đồ thị.
Tham khảo:
+ Leonard Euler's Solution to the Konigsberg Bridge Problem, Teo Paoletti http://www.maa.org/…/leonard-eulers-solution-to-the-konigsb…
+ How the Königsberg bridge problem changed mathematics, Dan Van der Vieren https://www.youtube.com/watch?v=nZwSo4vfw6c
hằng số toán học Euler-Mascheroni
Euler’s Sphere / Mặt cầu Euler

“Read Euler, read Euler, he is the master of us all!”, the great scientist Pierre-Simon Laplace
exclaimed so to express how big was Euler’s influence on mathematics.
My today story is about Euler’s Sphere, which I want to dedicate to
young readers who love mathematics.
“Hãy đọc Euler, hãy đọc Euler,
ông ấy là thầy của tất cả chúng ta!”, nhà đại bác học Pierre-Simon
Laplace kêu lên như thế để nói về ảnh hưởng lớn lao của Euler đối với
toán học. Câu chuyện của tôi hôm nay nói về Mặt Cầu Euler, như một món
quà dành cho các bạn trẻ yêu toán.
Tôi rất bất ngờ khi thống kê trên PVHg’s Home do WordPress.com thực hiện chỉ ra rằng bài báo “Lý thuyết giản lược về tứ diện” (A Brief Theory of Tetrahedron) là bài báo “ăn khách” nhất trên PVHg’s Home trong năm vừa qua, với 6.739 độc giả vào đọc.
Thực ra khi viết bài báo này, tôi chỉ có ý
định rất khiêm tốn là giúp MỘT học trò tôi quen biết củng cố kiến thức
môn toán, vì qua tiếp xúc, tôi thấy dường như học trò đó trống rỗng kiến
thức cơ bản, mặc dù đó là một học trò ngoan, chăm học của một trường
phổ thông được mô tả là có “tiếng tăm”. Không ngờ bài báo đó được nhiều
độc giả quan tâm (có lẽ phần lớn là những độc giả trẻ yêu toán). Thật
vậy, tính từ ngày được công bố trên PVHg’s Home, 11/08/2014, bài báo này
đến nay đã có 10.544 độc giả, đứng thứ nhì trong danh sách số độc giả
vào đọc (chỉ sau chủ đề Luận về Thiện/Ác).
Một độc giả tên là Anh (có lẽ là giáo
viên dạy toán?) bình luận, rằng bài báo nói trên là một “Sự tổng hợp
tuyệt vời, nhưng không biết học sinh phổ thông có nhớ nổi không”. Xin
chân thành cảm ơn bạn Anh. Câu hỏi liệu “học sinh có nhớ nổi hay không”
sẽ được thảo luận ở cuối bài viết này. Còn bây giờ, để đáp lại thịnh
tình của những độc giả trẻ yêu toán, tôi xin trình bày ngay câu chuyện
về Mặt Cầu Euler.
Nhưng trước khi phát biểu bài toán, tôi
xin có lời khuyên với các bạn trẻ, rằng sau khi đọc xong đầu bài, bạn
đừng nên đọc bất cứ một dòng nào của đáp án, dù chỉ là một đáp án gợi ý.
Thậm chí đừng “liếc mắt” vào hình vẽ trong đáp án. Bạn nên tự mình vẽ
hình và giải bài toán. Có bạn chỉ mất vài phút để tìm ra lời giải, có
bạn mất nhiều thời gian, nhưng bất kể thế nào bạn cũng nên tự mình có
đáp án của chính bạn. Chỉ sau khi có đáp án của chính mình mới tham khảo
đáp án của người khác. Bản thân tôi làm toán từ xưa đến nay đều như
thế, ngay cả sau này khi đã làm thầy giáo. Vì thế có bài toán tôi phải
mất vài năm mới tìm ra cách giải, thậm chí có bài toán không giải được,
nhưng tôi học được nhiều điều từ chính sự thất bại đó, vì để thất bại,
tôi đã có một sự quan sát công phu đối với vấn đề đang nghiên cứu. Tóm
lại, tôi luôn luôn cố gắng tìm đáp án của chính mình, thậm chí tự mình
tìm ra 2 hoặc nhiều đáp án khác nhau cho một bài toán. Khi ấy tôi mới
tham khảo đáp án của người khác. Theo tôi, đó là sự rèn luyện tác phong
làm khoa học, chuẩn bị tác phong tư duy độc lập, một phẩm chất cần phải
có đối với người làm khoa học sau này. Nhất là khi đã làm thầy, bạn phải
có đáp án của chính bạn, thay vì chỉ dựa dẫm vào những đáp án sẵn có.
Nhiều thầy cô giáo chỉ biết dựa vào những đáp án hướng dẫn nên khi dạy
học không có sức truyền cảm, vì khi ấy bạn không phải là thầy (the
master), mà chỉ là một chiếc máy nói, một chiếc loa phóng thanh. Ngược
lại, một người nói ra những ý kiến của chính mình bao giờ cũng sống
động, và do đó hấp dẫn lôi cuốn người nghe hơn rất nhiều so với những
chiếc máy nói.
Tóm lại, bạn hãy đọc BÀI TOÁN LỚN sau đây
rồi tự giải quyết trọn vẹn các câu hỏi trước khi đọc những phần tiếp
theo nhé. Bài toán bao gồm nhiều câu hỏi. Mục tiêu của câu chuyện hôm
nay là 2 câu hỏi cuối cùng, câu hỏi 7 và câu hỏi 8. Các câu hỏi trước đó
mang tính chất chuẩn bị.
(ĐÁP ÁN xem ở cuối bài viết này)
Vài nét về Leonard Euler
Leonhard Euler (1707 –1783) là một nhà
toán học Thụy Sĩ, đồng thời là nhà vật lý, thiên văn, nhà logic và kỹ sư
có rất nhiều khám phá quan trọng có ảnh hưởng lớn trong nhiều lĩnh vực
của toán học như giải tích vô cùng bé, lý thuyết đồ thị (graph theory),
đồng thời có những đóng góp đi tiên phong trong một số lĩnh vực khác như
lý thuyết topo, lý thuyết giải tích số (analytic number theory). Ông
cũng là người đưa vào toán học nhiều thuật ngữ và khái niệm mới, đặc
biệt trong toán học giải tích, chẳng hạn khái niệm hàm toán học. Ông
cũng nổi tiếng vì những công trình về cơ học, động lực học chất lỏng,
quang học, thiên văn và lý thuyết âm nhạc.
Euler là một trong những nhà toán học
xuất sắc nhất thế kỷ 18, và được xem như một trong những nhà toán học vĩ
đại nhất của mọi thời đại. Tập hợp các công trình của ông chất đầy
khoảng từ 60 đến 80 cuốn sách lớn, nhiều hơn bất kỳ một nhà toán học nào
khác.
Ông sống phần lớn thời gian ở St.
Petersburg, Nga, và Berlin, rồi ở thủ đô của Phổ. Câu nói nổi tiếng của
Pierre-Simon Laplace, một trong những nhà toán học – vật lý lớn nhất thế
kỷ 19, rằng “Hãy đọc Euler, hãy đọc Euler, ông là thầy của tất cả chúng
ta” (Read Euler, read Euler, he is the master of us all) có lẽ đủ để
nói lên tầm vóc của Euler.
Vai trò người thầy trong giáo dục
Theo tôi, học trò có nhớ nổi hay không là
do ở cách dạy – do ở thầy cô giáo, khi giảng bài trên lớp. Điều này
đúng với bất kỳ môn học nào, bất kỳ bài giảng nào.
Cách dạy nhồi nhét thuần túy kỹ thuật sẽ
làm cho học trò chán ngấy, và hình như đây là lối dạy học phổ biến hiện
nay trong nhiều môn học, thay vì chỉ riêng trong môn toán. Theo quan sát
của tôi, tình trạng này không chỉ có ở trường phổ thông, mà cả ở đại
học. Vì thế có rất nhiều học sinh bản chất thông minh nhưng kết quả học
tập vẫn kém. Tôi vô cùng ngạc nhiên khi thấy một học trò lớp 4 rất láu
lỉnh, tinh khôn, nhưng không thuộc bản cửu chương, không làm được phép
tính nhân với nhân tử có 2 chữ số, mặc dù cháu học ở một trường được đầu
tư khá nhiều về cơ sở vật chất. Tôi cũng biết hiện tượng học sinh lớp
10, 11, 12 không thuộc hằng đẳng thức đáng nhớ là phổ biến, mặc dù môn
toán các em được học ở trường là “toán nâng cao”. Đó là tình trạng dạy
giả và học giả kéo dài rất nhiều năm nay vẫn không sao chấm dứt. Theo
tôi, lỗi hoàn toàn thuộc về các nhà giáo dục, những người làm thầy thiên
hạ.
Tuy nhiên tôi cũng chứng kiến nhiều học
sinh bị coi là kém đã lấy lại được kiến thức rất nhanh khi gặp thầy
giáo thực sự giỏi – các em có sự thay đổi rõ rệt. Điều này chứng tỏ vai
trò người thầy quan trọng như thế nào. Rất tiếc là ở nhiều nước, chứ
không riêng Việt Nam, ngành sư phạm tuyển sinh vào trường với tiêu chuẩn
khá thấp, để rồi đào tạo ra những thầy cô giáo kém chất lượng. Đó là
một sai lầm mang tính chiến lược. Khi sự đã rồi, việc sửa chữa rất khó.
Một khi nền tảng cơ bản đã hỏng thì sửa chữa chỉ là chắp vá.
Một lần, một hiệu trưởng một trường đại
học nói với tôi rằng sinh viên trường ông nói chung là kém. Tôi không
ngần ngại trả lời: “Không, thưa ông, tôi không nghĩ thế, vì khi tiếp xúc
với sinh viên, tôi thấy các em rất nhanh nhẹn, thông minh. Nếu các em
kém, ấy là vì chúng ta, chính các thầy giáo chúng ta kém chứ không phải
học trò. Nếu thầy giỏi, chắc chắn học trò cũng giỏi”.
Thật vậy, nếu người thầy biết đánh thức
học trò bằng ý nghĩa thực tế, ý nghĩa văn hóa, ý nghĩa lịch sử và thậm
chí cả ý nghĩa triết học của những vấn đề học thuật mà thầy đang dạy thì
bất cứ học trò nào cũng thích thú để học, và do đó sẽ nắm được bài học
một cách dễ dàng và thấu đáo, vì khi đó các em sẽ chủ động tìm hiểu
những vấn đề các em muốn biết. Muốn thế người thầy đúng nghĩa phải là
một người không chỉ giỏi về chuyên môn, mà còn phải có một vốn văn hóa,
một vốn hiểu biết rộng và sâu sắc về thế giới. Khi đó, những điều thầy
nói với trò không phải là dạy dỗ trò, mà là truyền cảm cho học trò –
truyền cho học trò niềm cảm hứng say mê của chính mình về ý nghĩa và cái
đẹp của thế giới. Niềm say mê đó có sức lay chuyển, rung động những tâm
hồn vốn trong sáng của học trò. Vấn đề là người thầy có đủ những phẩm
chất đó hay không.
Học sinh của tôi mấy chục năm trước đây
không những có thể nhớ nổi những kiến thức phức tạp mà còn làm chủ được
những kiến thức đó, biến nó thành tài sản tri thức của chính các em sau
này, không chỉ đối với lý thuyết về tứ diện, mà còn nhiều lý thuyết khác
rất thú vị trong môn toán nói riêng và khoa học nói chung nữa.
Tóm lại, đừng lo học trò có nhớ nổi bài
giảng hay không. Hãy lo làm sao người thầy có đủ phẩm chất của người
thầy. Đây là trách nhiệm của ngành giáo dục.



45-Alessandro Volta
1745-1827
Ý
Vật Lý, Hóa Học
Alessandro Volta: Nhà khoa học người Ý lỗi lạc
Bá tước Alessandro Giuseppe Antonio Anastasio Volta (18 tháng 2 năm 1745 - 5 tháng 5 năm 1827) là một nhà vật lý người Ý. Ông là người đã có công phát minh ra pin điện và tên của ông được đặt theo đơn vị điện thế volt (ký hiệu V).
Alexandro Volta, từ nhỏ đã say mê khoa
học tự nhiên, năm 29 tuổi ông đã trở thành giảng viên vật lý cho một
trương trung học ở quê hương ông cho đến năm 1779. Sau những cố gắng
hoài công nhằm hòa giải các thuyết đã biết, nhà bác học trẻ tuổi chú tâm
vào cá ứng dụng trực tiếp của điện học. Những văn kiện nay vẫn còn nổi
tiếng chứng tỏ hoạt động của ông. Đó là những văn kiện liên lạc gửi cho
nhà điện học Beccaria và nhà vạn vật học Spallanzani, được xem như những
nhà chuyên môn vĩ đại nhất của thời họ trong hai lĩnh vực này. Còn lúc
này Volta chỉ mới 24 tuổi!
Alexandro Volta (18/2/1745 - 5/5/1827)
Kể từ 1796 trở đi, các trực giác của
thiên tài Volta nối tiếp nhau: Chính các trực giác này đã đóng một vai
trò quyết định vào những cuộc khảo cứu và khám phá của những năm kế
tiếp. Các khám phá này là kết quả của biết bao kinh nghiệm rút từ các sự
thu lượm mới mẻ trước.
Dẫu cho Volta không sáng chế ra loại pin
điện mang tên ông, ông cũng vẫn được xếp vào hàng đầu trong lịch sử Vật
Lý nhờ phát minh “Bình phát cảm ứng điện vĩnh cửu” (1775) mà
ông gọi là nguồn gốc các động cơ cảm ứng từ tương lai. Ngoài ra, nhân
lọai còn mang ơn ông đã sáng chế ra khí nhiên kế, mà ngày nay dùng để đo
lượng oxygen có trong không khí; máy đọng điện (1782) và máy điện
nghiệm. Cũng chính ông là người đầu tiên khám phá ra khí bốc từ các đầm
lầy, mà ngày nay gọi là khí mêtan –CH4.
Một số mốc thời gian quan trọng trong cuộc đời Alexandro Volta:
1774: ông trở thành
giáo sư vật lý tại trường Khoa học hoàng gia ở Cosmo và trong những năm
tiếp theo ông phát minh ra Electrophorus: thiết bị tạo ra dòng điện nhờ
ma sát giữa đĩa và một bản kim loại.
1776-1777: ông tập trung nghiên cứu hoá học, nghiên cứu dòng điện trong chất khí và lập những thí nghiệm như sự phóng điện trong bình kín.
1779: ông trở thành giáo sư khoa vật lý trường đại học Pavia trong suốt 25 năm.
1800: Volta phát minh pin điện hoá (pin Volta), cha đẻ của pin hoá học hiện đại, tạo ra dòng điện ổn định.
Năm 1823, cái chết đau đớn của một đứa
con đã gây cho ông xúc động quá mạnh khiến những ngày còn lại của ông
trên cõi đời càng rút ngắn hơn. Vào ngày 5/03/1827, một ngôi sao sáng
trên thế giới khoa học đã tắt lịm. Thiên tài Volta ra đi đã để lại cho
thế hệ sau một hướng đi mới, để thay đổi sâu rộng cả một thế giới mà ông
không bao giờ ngờ tới cũng như không bao giờ có thể được chứng kiến.
Alessandro Volta - người phát minh ra pin điện
Đơn vị điện thế Volt (ký hiệu V) được đặt theo tên của bá
tước, nhà Vật lý học người Ý Alessandro Volta. Ông chính là người đã
phát minh ra pin điện.

Alessandro Volta - Ảnh: en.wikipedia.org
Alessandro Volta sinh ngày 18/02/1745 tại Como, nước Ý. Ông say mê khoa học tự nhiên ngay từ khi còn nhỏ.
Năm 24 tuổi, Volta viết một quyển sách bàn về sức hút của điện được giới khoa học hết sức chú ý.
Bước sang tuổi 29, Volta trở thành giảng viên Vật lý tại trường Khoa học Hoàng gia ở Cosmo. Trong những năm tiếp theo, Volta phát minh ra Electrophorus - thiết bị tạo ra dòng điện nhờ ma sát giữa đĩa và một bản kim loại.
Trong 2 năm 1776 và 1777, Volta tập trung nghiên cứu hoá học, nghiên cứu dòng điện trong chất khí và lập những thí nghiệm như sự phóng điện trong bình kín.
Năm 1779, Volta trở thành giáo sư giảng dạy môn Vật lý tại trường Đại học Pavia và là hiệu trưởng của trường vào năm 1795.
Alessandro Volta là một trong những người phản đối giả thuyết “điện sinh vật” của Galvani. Vào năm 1791, nhiều phòng thí nghiệm lớn tại Châu Âu, hàng loạt các nhà khoa học đã thực hiện các thí nghiệm với đôi chân nhái của Galvani. Đối với thí nghiệm chân nhái, Volta không quan tâm đến hiện tượng co giật đơn thuần, ông miệt mài trong việc tìm hiểu nguồn điện đã sinh ra từ đâu để làm chân nhái có thể co giật. Volta nhận thấy chân nhái chỉ co giật khi có sự tiếp xúc của 2 kim loại khác nhau. Sau hàng loạt các nghiên cứu, Volta phát hiện điện sinh ra do phản ứng hóa học và hiện tượng co giật của chân nhái chỉ xảy ra khi 2 kim loại khác nhau tiếp xúc trong một dung dịch muối. Cụ thể, dung dịch muối tồn tại bên trong cơ thịt của chân nhái.
Mô hình pin của Volta
Năm 1800, Volta thực hiện một loạt các thử nghiệm dùng kẽm, chì, thiếc và sắt làm tấm tích điện âm (cathode); và đồng, bạc, vàng, than chì như một tấm tích điện dương (anode). Sau đó, ông xếp các tấm trái cực xen kẽ với nhau, ngăn cách bởi miếng giấy xốp tẩm dung dịch muối ăn. Cuối cùng, ông nối điểm đầu và điểm cuối với một sợi dây dẫn và nhận thấy có một dòng điện chạy qua. Đây chính là viên pin đầu tiên của nhân loại được mang tên là “pin Volta”. Sở dĩ danh từ pin hay chính xác hơn là pile được đặt cho thiết bị này chính là do đây là một chồng các miếng tròn bằng đồng và kẽm có hình dáng như một chiếc cọc.

Mô hình pin đầu tiên của Volta còn được bảo tồn đến ngày nay
Với phát minh của mình, Volta giúp con người bắt đầu có được nguồn
điện một chiều ổn định. Ông được ghi nhận là người có đóng góp to lớn
cho sự phát triển của nhân loại, mở rộng lĩnh vực nghiên cứu của điện
học từ chỗ chỉ nghiên cứu tĩnh điện mở rộng sang nghiên cứu động điện,
điện hóa học...
Volta mất vào ngày 05/3/1827. Đơn vị điện thế Volt được đặt theo tên của ông cho đến tận ngày nay.
Alessandro Volta - Ảnh: en.wikipedia.org
Năm 24 tuổi, Volta viết một quyển sách bàn về sức hút của điện được giới khoa học hết sức chú ý.
Bước sang tuổi 29, Volta trở thành giảng viên Vật lý tại trường Khoa học Hoàng gia ở Cosmo. Trong những năm tiếp theo, Volta phát minh ra Electrophorus - thiết bị tạo ra dòng điện nhờ ma sát giữa đĩa và một bản kim loại.
Trong 2 năm 1776 và 1777, Volta tập trung nghiên cứu hoá học, nghiên cứu dòng điện trong chất khí và lập những thí nghiệm như sự phóng điện trong bình kín.
Năm 1779, Volta trở thành giáo sư giảng dạy môn Vật lý tại trường Đại học Pavia và là hiệu trưởng của trường vào năm 1795.
Alessandro Volta là một trong những người phản đối giả thuyết “điện sinh vật” của Galvani. Vào năm 1791, nhiều phòng thí nghiệm lớn tại Châu Âu, hàng loạt các nhà khoa học đã thực hiện các thí nghiệm với đôi chân nhái của Galvani. Đối với thí nghiệm chân nhái, Volta không quan tâm đến hiện tượng co giật đơn thuần, ông miệt mài trong việc tìm hiểu nguồn điện đã sinh ra từ đâu để làm chân nhái có thể co giật. Volta nhận thấy chân nhái chỉ co giật khi có sự tiếp xúc của 2 kim loại khác nhau. Sau hàng loạt các nghiên cứu, Volta phát hiện điện sinh ra do phản ứng hóa học và hiện tượng co giật của chân nhái chỉ xảy ra khi 2 kim loại khác nhau tiếp xúc trong một dung dịch muối. Cụ thể, dung dịch muối tồn tại bên trong cơ thịt của chân nhái.
Mô hình pin của Volta
Năm 1800, Volta thực hiện một loạt các thử nghiệm dùng kẽm, chì, thiếc và sắt làm tấm tích điện âm (cathode); và đồng, bạc, vàng, than chì như một tấm tích điện dương (anode). Sau đó, ông xếp các tấm trái cực xen kẽ với nhau, ngăn cách bởi miếng giấy xốp tẩm dung dịch muối ăn. Cuối cùng, ông nối điểm đầu và điểm cuối với một sợi dây dẫn và nhận thấy có một dòng điện chạy qua. Đây chính là viên pin đầu tiên của nhân loại được mang tên là “pin Volta”. Sở dĩ danh từ pin hay chính xác hơn là pile được đặt cho thiết bị này chính là do đây là một chồng các miếng tròn bằng đồng và kẽm có hình dáng như một chiếc cọc.
Mô hình pin đầu tiên của Volta còn được bảo tồn đến ngày nay
Volta mất vào ngày 05/3/1827. Đơn vị điện thế Volt được đặt theo tên của ông cho đến tận ngày nay.
An Nguyễn
(Tổng hợp)
(Tổng hợp)
Bí ẩn về đời sống tâm linh của các thiên tài nổi tiếng (Kỳ 5)
Chủ nhật, 23/07/2017 11:00
Volta - người khai sinh ra pin điện là một trong nhiều nhà khoa học có niềm tin mạnh mẽ vào Chúa.
Alessandro Volta (1745 - 1827) là nhà vật lý vĩ đại
người Ý phát minh ra pin điện - năng lượng đã làm thay đổi cả thế giới.
Để nhớ đến công lao to lớn này của ông, khoa học đã đặt tên cho đơn vị
điện thế là volt theo tên của ông (ký hiệu V).
Chân dung Volta, cha đẻ của pin điện
Thủa nhỏ, Volta là cậu bé chậm nói, thậm
chí lên 4 tuổi vẫn chưa thể cất lên lời khiến cha mẹ lo lắng. Tuy nhiên,
Volta lại tỏ ra tò mò với mọi thứ xung quanh.
7 tuổi, Volta mới nói năng trôi chảy nhưng
khi đó, cha của Volta không may qua đời. Cậu bé được người chú là một
thầy tu nuôi nấng, chăm chút như con đẻ và đặc biệt rất quan tâm tới
việc học hành của Volta.
Chú Volta mua rất nhiều sách, khuyến khích Volta đọc và cho cậu bé theo học trường dòng. Dần dần, Volta bộc lộ rõ niềm say mê khoa học tự nhiên.
Năm 24 tuổi, Volta viết sách về sức hút
của điện thu hút được sự chú ý của giới chuyên môn. 29 tuổi, ông đã trở
thành giảng viên vật lý ở trường Hoàng gia tại Cosmo - quê hương ông và
dạy ở đó trong 5 năm.
Năm 1779, Volta dạy vật lý ở trường đại học Pavia. 16 năm sau, ông trở thành hiệu trưởng của trường.
Có lẽ do ảnh hưởng từ người chú, lại nhận được sự giáo dục từ trường Công giáo nên Volta đã là một tín đồ Kito giáo từ bé. Ông đọc nhiều sách về Kinh thánh và khoa học, tin rằng Chúa trời đã chỉ lối cho ông đi đúng hướng: "Tôi tạ ơn Chúa đã ban cho tôi đức tin này, nhờ đó mà tôi có một ý hướng vững chắc để sống và chết".
Năm 1769, cuốn sách về điện đầu tay của
ông được xuất bản tuy không phải là những khám phá khoa học mới mẻ nhưng
lại chứa đựng những kiến thức cơ bản nhất mà Volta nghiên cứu được, là
tiền đề cho các phát minh của ông về sau.
Năm 1800, thí nghiệm điện cực dẫn của ông
cho ra đời viên pin đầu tiên, được gọi là pin volta, về sau được cải
biến thành pin điện ngày nay. Hình dáng của pin volta như một chiếc cọc,
bên trong có chứa nhiều miếng tròn bằng đồng và kẽm chồng lên nhau, có
thể tạo ra dòng điện liên tục. Nhờ có phát minh này của ông mà nhân loại
đã có được dòng điện một chiều để sử dụng.
Ngày nay, mô hình pin Volta vẫn được bảo tồn
Sau thành công của pin điện, Volta được
tôn vinh là người tạo ra bước đột phá mới cho nền khoa học. Dù ở thời
điểm đó, con người vẫn còn có sự phân biệt rõ ràng giữa duy vật và duy
tâm. Người ta tin rằng khoa học là chủ nghĩa duy vật, còn đạo là duy
tâm. Nhưng nhà khoa học vĩ đại Volta đã công khai bảo vệ tín ngưỡng của
ông. "Tôi không bao giờ thấy mình bị dao động trong đức tin", Volta khẳng định.
Năm 1801, Volta được hoàng đế Napoleon mời
sang Pháp để giảng dạy ở Viện hàn lâm Paris. Về sau, ông được phong
chức bá tước. Cho đến nay, người ta nhắc tới Volta không chỉ với danh
nghĩa nhà khoa học mà còn bằng cái tên đầy kính trọng "Bá tước
Alessandro Volta".
LEO
Theo Vietnamnet
Theo Vietnamnet
Câu chuyện về những con người làm nên ngành Điện
Điện bắt đầu từ đâu, ai là người đầu tiên tạo ra Điện, ngành Điện phát triển như thế nào.... bài viết sau đây sẽ giải đáp phần nào những thắc mắc trên.
Thalès de Milet
Một trong các sự kiện quan trọng đầu tiên có thể bắt đầu vào khoảng 600 năm trước công nguyên khi nhà triết gia Hy Lạp tên Thales sống tại Miletus phát hiện ra rằng khi cọ sát thanh Hổ Phách vào da hoặc len thì nó bắt đầu hút được các sợi nhỏ như giấy, sợi vải (hiệu ứng tĩnh điện, the tribo-electric effect) và khi cọ sát một thời gian đủ lâu nó bắt đầu phát sinh ra nhiệt rồi xuất hiện tia lửa.
Thalès de Milet (khoảng 624-546 TCN)(1)
Gần thành phố Magnesia của Hy lạp cổ đại có một loại đá đặc biệt được gọi là đá Magnesia có chứa magnetite (sắt từ Fe2O3) loại đá này có khả năng hút lẫn nhau và hút được các vật làm bằng sắt.
Alessandro Volta người phát minh ra pin điện
Alessandro Volta, hay Count Alessandro Giuseppe Antonio Anastasio Volta là nhà vật lý tiên phong nghiên cứu về điện, sinh tại Como, Lombardy, Italy năm 1745.(2)
Alessandro Volta
Vào năm 1780, Louis Galvani (1737- 1798) một nhà sinh học, đang dạy môn giải phẫu học tại Đại học Bologna đã tình cờ thấy rằng những con ếch bị giết do co rút bắp thịt khi có kim loại chạm vào, Volta thử lại thí nghiệm của Galvani và đã phát hiện ra rằng cơ thể con ếch chỉ là một chất dẫn điện thường. Chính điện sinh ra trong các kim loại dị chất đã kích thích các dây thần kinh, và làm hoạt động các cơ.
Thí nghiệm của Galvani
Năm 1794 Volta bắt đầu quyết tâm tìm ra phương pháp tạo ra dòng điện mà không cần sử dụng đến các mô động vật.
Đến năm 1800 Volta phát hiện ra rằng bằng cách đặt hai mẫu kim loại khác nhau vào ly nước muối (nước cất và muối) điện được tạo ra, từ những bước đầu đó ông bắt đầu nghiên cứu và phát minh ra pin điện, sau sự kiện này ông nổi danh trên toàn thế giới và tên của ông được đặt cho một đơn vị mà dân điện nào cũng biết Volt
Pin Volta
Pin Volta là một tấm kẽm và một tấm đồng nhúng trong axit sunfuric, nếu nối hai tấm kim loại này với nhau thì nó có thể sản sinh ra dòng điện liên tục và ổn định. Alessandro Volta đã trình diện phát minh này với Napoleon Bonaparte tại Paris vào ngày 6 tháng 11 năm 1801.
André Marie Ampère
André-Marie Ampère đã được sinh ra ở Lyon Phápnăm 1775. Ông không bao giờ đi học và sự giáo dục duy nhất anh nhận được là bởi cha mình, một thương gia chuyên nghiệp, chuyên gia trong tiếng Latin và văn học Pháp. Ngay khi còn trẻ ông đã chứng tỏ mình là một thần đồng, ở tuổi 12 ông đã thông thạo toán học cơ bản đặc biệt là vi phân và tích phân, ai nói là muốn giỏi thì nhất định là phải đến trường đâu phải không.
André Marie Ampère(1775-1836)
Năm 1825 dựa vào phát hiện của Ørsted năm 1820 về tác dụng của dòng địện lên kim nam châm, ông đã nghiên cứu bằng thực nghiệm, tìm ra lực điện từ và phát biểu thành Định luật Ampère. Lực điện từ là một trong các lực cơ bản của tự nhiên, cơ sở của điện động lực học. Định luật Ampère cho phép xác định chiều và trị số của lực điện từ, là cơ sở chế tạo động cơ điện. Công thức Ampère và định luật Faraday là hai cơ sở chính để James Clerk Maxwell xây dựng nên lý thuyết trường điện từ.
Ampère đã phát biểu quy tắc xác định từ trường của dòng điện (quy tắc vặn nút chai), tiên đoán dòng điện phân tử để giải thích bản chất từ của vật liệu sắt từ. Sau Ampère, vật liệu sắt từ trở nên rất phổ biến và ông cũng chính là người phát minh ra điện kế, nền tảng cho các công cụ đo điện hiện nay.
Điện kế (Galvanometer)
Michael Faraday
Michael Faraday
Michael Faraday, FRS (22/9/1791 – 25/8/1867) là một nhà hóa học và vật lý học người Anh (hoặc là nhà triết học tự nhiên, theo thuật ngữ của thời đó) đã có công đóng góp cho lĩnh vực Điện từ học và Điện hóa học.
Chú thích:
(1) Thalès de Milet hay theo phiên âm tiếng Việt là Ta-lét , là một triết gia, một nhà toán học người Hy Lạp sống trước Socrates, người đứng đầu trong bảy nhà hiền triết của Hy Lạp. Ông cũng được xem là một nhà triết gia đầu tiên trong nền triết học Hy Lạp cổ đại, là "cha đẻ của khoa học". Tên của ông được dùng để đặt cho một định lý toán học do ông phát hiện ra.
(2) Bá tước Alessandro Giuseppe Antonio Anastasio Volta (18 tháng 2 năm 1745 - 5 tháng 5 năm 1827) là một nhà vật lý người Ý. Ông là người đã có công phát minh ra pin điện và tên của ông được đặt theo đơn vị điện thế volt (ký hiệu V).
Bài viết đang cập nhật...
Khám phá lịch sử hình thành và phát triển của pin
(GenK.vn) - Pin là nguồn năng lượng thông dụng cho nhiều thiết bị cá nhân, gia dụng cho đến các ứng dụng công nghiệp.
Pin
là nguồn năng lượng thông dụng cho nhiều thiết bị cá nhân, gia dụng cho
đến các ứng dụng công nghiệp. Có nhiều chủng loại, kích thước pin khác
nhau tương ứng với rất nhiều thiết bị tiêu thụ điện từ đồng hồ đeo tay,
đồ chơi trẻ em, điện thoại di động, máy tính bảng đến pin cỡ lớn dùng
cho xe điện,... Pin đã, đang và sẽ là một công cụ lưu trữ năng lượng
được sử dụng phổ biến không chỉ trong hiện tại mà còn nhiều năm nữa
trong tương lai. Chuyên mục " Mỗi tuần 1 phát minh
" lần này sẽ cùng các bạn tìm hiểu các câu hỏi đặt ra xung quanh loại
thiết bị quen thuộc và quan trọng nói trên: Pin được chế tạo lần đầu
tiên khi nào? Ai đã phát minh ra pin? Pin sạc có từ bao giờ?...
Tóm tắt các cột mốc quan trọng có liên quan mật thiết đến quá trình phát triển của pin
 Pin được phát minh khi nào? 400 năm hay hơn 2000 năm trước?
Pin được phát minh khi nào? 400 năm hay hơn 2000 năm trước?
Một trong những phát minh vĩ đại và đáng chú ý nhất của con người trong 400 năm qua chính là điện. Những dòng điện đầu tiên có thể được tạo ra trước đó, nhưng mãi đến cuối những năm 1800 thì nhân loại mới chứng kiến được những ứng dụng cụ thể của điện. Đó là 250.000 bóng đèn dây tóc thắp sáng Triễn lãm tiêu dùng tại Chicago, Mỹ năm 1893 hay làm một cây cầu bắt qua sông Seine, Paris phát sáng tại Hội chợ thế giới năm 1900.
Tuy nhiên, những dòng điện đầu tiên đã được con người tạo ra từ nhiều năm trước đó. Vào năm 1963, trong quá trình xây dựng tuyến đường sắt gần Baghdad, những công nhân đã phát hiện ra những "viên pin của người Parthian" có niên đại lên tới 2000 năm nằm trong một hầm mộ cổ. Đây là những viên pin xuất hiện sớm nhất trong lịch sử loài người do bàn tay chế tạo của những người Parthian, một dân tộc miền Bắc Ba Tư.
 Trong số những di tích được tìm thấy trong lăng mộ, các nhà khảo cổ
đã tìm thấy một cái vại hoặc bình bằng đất sét chứa đầy giấm với một
thanh sắt cắm vào chính giữa sau đó niêm phong kính miệng bình. Xung
quanh thanh sắt được bao bọc bởi ống quấn bằng các tấm đồng. Mỗi bình có
chiều cao khoảng 15 cm, ống đồng có đường kính khoảng 4 cm và dài 12
cm. Sau khi dựng lại và thử nghiệm với một phiên bản tương tự, các nhà
khoa học đã nhận thấy rằng "bình pin" có khả năng tạo ra dòng điện từ
1,5 đến 2 V giữa trụ sắt và tấm đồng.
Trong số những di tích được tìm thấy trong lăng mộ, các nhà khảo cổ
đã tìm thấy một cái vại hoặc bình bằng đất sét chứa đầy giấm với một
thanh sắt cắm vào chính giữa sau đó niêm phong kính miệng bình. Xung
quanh thanh sắt được bao bọc bởi ống quấn bằng các tấm đồng. Mỗi bình có
chiều cao khoảng 15 cm, ống đồng có đường kính khoảng 4 cm và dài 12
cm. Sau khi dựng lại và thử nghiệm với một phiên bản tương tự, các nhà
khoa học đã nhận thấy rằng "bình pin" có khả năng tạo ra dòng điện từ
1,5 đến 2 V giữa trụ sắt và tấm đồng.
Qua đó, các nhà khoa học đã dự đoán rằng những người Parthian cổ đại đã sử dụng các công cụ tạo ra dòng điện để mạ vàng và bạc vào những vật dụng từ những năm 250 trước công nguyên. Nhiều nhà khoa học cho rằng người Parthian chỉ sử dụng các công cụ trên cho mục đích mạ chứ chưa nhìn nhận nó như một nguồn năng lượng. Nhiều bằng chứng khảo cổ khác cho thấy những người Ai Cập cổ đại cũng đã biết mạ antimon lên các vật dụng bằng đồng từ hơn 4300 năm trước. Các di tích khảo cổ khác cũng cho thấy những người Babylon cũng đã khám phá và sử dụng kỹ thuật dùng nước ép nho như một chất điện phân để mạ vàng lên đồ trang sức.
1786 - Cặp chân nhái đã chết nhưng biết cử động!
 Năm 1786, trong khi thực hiện một bài giảng, giáo sư Cơ thể học Luigi
Galvani (1737-1798) tại trường Đại học Bologne, Italy, đã dùng một
thanh kim loại đâm vào một con nhái đã lột da. Do tình cờ con nhái được
đặt trên mặt bàn bằng kim loại, chân con nhái có hiện tượng co giật lại.
Galvani đã rất ngạc nhiên với hiện tượng này và sau vài ngày tìm hiểu,
ông đã nhận ra rằng chân nhái co giật khi đầu thanh kim loại đâm vào và
chạm tới mặt bàn kim loại bên dưới.
Năm 1786, trong khi thực hiện một bài giảng, giáo sư Cơ thể học Luigi
Galvani (1737-1798) tại trường Đại học Bologne, Italy, đã dùng một
thanh kim loại đâm vào một con nhái đã lột da. Do tình cờ con nhái được
đặt trên mặt bàn bằng kim loại, chân con nhái có hiện tượng co giật lại.
Galvani đã rất ngạc nhiên với hiện tượng này và sau vài ngày tìm hiểu,
ông đã nhận ra rằng chân nhái co giật khi đầu thanh kim loại đâm vào và
chạm tới mặt bàn kim loại bên dưới.
Một ngày khác, Galvani đã dùng một móc đồng phơi đôi chân nhái phía trên một thanh sắt ngoài ban công. Galvani đã nhận thấy rằng khi gió thổi khiến đôi chân nhái đung đưa chạm vào thanh sắt và ngay tức khắc, chân nhái sẽ bị co giật. Ông suy nghĩ để cố lý giải cho hiện tượng kỳ lạ này và một ý tưởng đã lóe lên trong đầu ông: điện. Galvani kết luận rằng điện có trong khắp mọi vật và có trong cả đôi chân nhái. Ông đặt tên cho loại điện này là "điện của sinh vật" và công bố phát hiện của mình trên một bài báo khiến cho giới khoa học gia châu Âu hết sức sửng sốt với loại điện mới này.
Ngày nay, chúng ta đều biết rằng Galvani đã nhầm lẫn khi cho rằng đó là điện của sinh vật và ông chỉ dừng lại ở hiện tượng mà không tìm hiểu nguyên nhân sinh ra điện. Tuy nhiên, phát hiện trên của Galvani đã tiến rất gần tới những nguyên lý mở đường cho việc chế tạo pin sau này.
"Pin Volta" - Pin đầu tiên của nhân loại ra đời vào năm 1800
 Alessandro Volta (1745-1827) là giáo sư vật lý tại Đại học Pavie,
Italy. Trước đó, Volta đã có nhiều nghiên cứu nhằm tăng cường tính điện
của chai Laiden. Trước đó, ông đã đề xuất mô hình "súng lục bắn điện"
nhằm thực hiện liên lạc đường dài. "Khẩu súng lục điện" được nối với một
sợi dây sắt và đặt trên các cọc gỗ kéo dài từ Milan đến Como, Italy.
Đầu cuối của dây sắt được nối với một chai chứa đầy khí mêtan. Khi muốn
gởi một thông điệp được mã hóa, "súng lục điện" sẽ "bắn" một tia lửa
điện và người nhận sẽ "đọc" được các thông điệp trên chai chứa mêtan. Dù
vậy, mô hình của ông không hề được chế tạo thực sự.
Alessandro Volta (1745-1827) là giáo sư vật lý tại Đại học Pavie,
Italy. Trước đó, Volta đã có nhiều nghiên cứu nhằm tăng cường tính điện
của chai Laiden. Trước đó, ông đã đề xuất mô hình "súng lục bắn điện"
nhằm thực hiện liên lạc đường dài. "Khẩu súng lục điện" được nối với một
sợi dây sắt và đặt trên các cọc gỗ kéo dài từ Milan đến Como, Italy.
Đầu cuối của dây sắt được nối với một chai chứa đầy khí mêtan. Khi muốn
gởi một thông điệp được mã hóa, "súng lục điện" sẽ "bắn" một tia lửa
điện và người nhận sẽ "đọc" được các thông điệp trên chai chứa mêtan. Dù
vậy, mô hình của ông không hề được chế tạo thực sự.
Từ khi Galvani phổ biến các phát hiện của mình về "điện của sinh vật" vào năm 1791, tại nhiều phòng thí nghiệm lớn tại châu Âu, hàng loạt các nhà khoa học đã thực hiện các thí nghiệm với đôi chân nhái của Galvani. Có người đã nối đôi chân nhái với chai Leiden (hình thái đầu tiên của tụ điện, một chai thủy tinh tích trữ tĩnh điện giữa 2 điện cực bên trong và bên ngoài chai) và nhận thấy rằng đôi chân nhái có sự co giật dữ dội. Với thí nghiệm trên, các nhà khoa học bắt đầu nghi ngờ về giả thuyết "điện sinh vật" của Galvani. Trong số những người phản đối giả thuyết có Alessandro Volta.
Đối với thí nghiệm chân nhái , Volta không quan tâm đến hiện tượng co giật đơn thuần, sâu xa hơn, ông cố gắng tìm hiểu nguồn điện đã sinh ra từ đâu để làm chân nhái có thể co giật. Volta nhận thấy rằng chân nhái chỉ co giật khi có sự tiếp xúc của 2 kim loại khác nhau. Sau khi tiếp tục nghiên cứu, Volta phát hiện thêm rằng điện sinh ra do phản ứng hóa học và hiện tượng co giật của chân ếch chỉ xảy ra khi 2 kim loại khác nhau tiếp xúc trong một dung dịch muối. Cụ thể, dung dịch muối tồn tại bên trong cơ thịt của chân nhái.
 Tiếp tục nghiên cứu, năm 1800, Volta đã thực hiện một loạt các thử
nghiệm dùng kẽm, chì, thiếc và sắt làm tấm tích điện âm (cathode); và
đồng, bạc, vàng, than chì như một tấm tích điện dương (anode). Sau đó,
ông xếp các tấm trái cực xen kẽ với nhau, ngăn cách bởi miếng giấy xốp
tẩm dung dịch muối ăn. Cuối cùng, ông nối điểm đầu với điểm cuối với một
sợi dây dẫn và nhận thấy có 1 dòng điện chạy qua. Đây chính là viên pin
đầu tiên của nhân loại được mang tên là "pin Volta". Sở dĩ danh từ pin
hay chính xác hơn là pile được đặt cho thiết bị này chính là do đây là 1
chồng các miếng tròn bằng đồng và kẽm có hình dáng như một chiếc cọc.
Tiếp tục nghiên cứu, năm 1800, Volta đã thực hiện một loạt các thử
nghiệm dùng kẽm, chì, thiếc và sắt làm tấm tích điện âm (cathode); và
đồng, bạc, vàng, than chì như một tấm tích điện dương (anode). Sau đó,
ông xếp các tấm trái cực xen kẽ với nhau, ngăn cách bởi miếng giấy xốp
tẩm dung dịch muối ăn. Cuối cùng, ông nối điểm đầu với điểm cuối với một
sợi dây dẫn và nhận thấy có 1 dòng điện chạy qua. Đây chính là viên pin
đầu tiên của nhân loại được mang tên là "pin Volta". Sở dĩ danh từ pin
hay chính xác hơn là pile được đặt cho thiết bị này chính là do đây là 1
chồng các miếng tròn bằng đồng và kẽm có hình dáng như một chiếc cọc.
 Cũng trong năm 1800, Volta đã công bố phát hiện của ông về một nguồn
cấp điện ổn định trước Hội đồng khoa học Hoàng Gia tại London trước sự
chứng kiến và thán phục của nhiều nhà khoa học từ khắp châu Âu. Với phát
minh này đã giúp tên tuổi của Volta lừng lẫy khắp nơi và được ghi nhận
là người có đóng góp to lớn cho sự phát triển của nhân loại.
Cũng trong năm 1800, Volta đã công bố phát hiện của ông về một nguồn
cấp điện ổn định trước Hội đồng khoa học Hoàng Gia tại London trước sự
chứng kiến và thán phục của nhiều nhà khoa học từ khắp châu Âu. Với phát
minh này đã giúp tên tuổi của Volta lừng lẫy khắp nơi và được ghi nhận
là người có đóng góp to lớn cho sự phát triển của nhân loại.
 Tuy nhiên, Pháp mới là quốc gia đầu tiên công nhận phát minh của
Volta do trong giai đoạn bấy giờ, nước Pháp đang cố gắng tiếp cận với
nhiều tiến bộ của khoa học kỹ thuật nên sẵn sàng đón nhận bất cứ ý tưởng
mới nào được đề xuất. Không lâu sau đó, Volta được mời tới Pháp và
giảng dạy tại Viện hàn lâm khoa học Pháp về các nghiên cứu điện học của
ông. Thậm chí trong nhiều bài giảng của ông có sự theo dõi của Napoleon
Bonaparte.
Tuy nhiên, Pháp mới là quốc gia đầu tiên công nhận phát minh của
Volta do trong giai đoạn bấy giờ, nước Pháp đang cố gắng tiếp cận với
nhiều tiến bộ của khoa học kỹ thuật nên sẵn sàng đón nhận bất cứ ý tưởng
mới nào được đề xuất. Không lâu sau đó, Volta được mời tới Pháp và
giảng dạy tại Viện hàn lâm khoa học Pháp về các nghiên cứu điện học của
ông. Thậm chí trong nhiều bài giảng của ông có sự theo dõi của Napoleon
Bonaparte.
 Trong cùng năm 1800, nhà vật lý và hóa học người Cornwall, vương quốc
Anh, Humphry Davy (1778-1829) đã bắt đầu thử nghiệm các tác dụng hóa
học của dòng điện và phát hiện ra rằng dòng điện có khả năng tách các
chất trong dung dịch mà ngày nay chúng ta biết đó là sự điện phân. Dựa
trên mô hình của Volta, Davy đã chế tạo ra pin điện lớn nhất và mạnh
nhất tính đến thời điểm bấy giờ tại tầng hầm của Viện khoa học Hoàng gia
Anh. Những nhân chứng đã kể lại rằng mô hình pin của ông đã làm một
chiếc đèn hồ quang điện chat sáng rực rỡ chưa từng thấy. Ngoài ra, Davy
cũng là người nổi tiếng với việc phát hiện ra khí gây cười N2O hay đèn
mỏ an toàn.
Trong cùng năm 1800, nhà vật lý và hóa học người Cornwall, vương quốc
Anh, Humphry Davy (1778-1829) đã bắt đầu thử nghiệm các tác dụng hóa
học của dòng điện và phát hiện ra rằng dòng điện có khả năng tách các
chất trong dung dịch mà ngày nay chúng ta biết đó là sự điện phân. Dựa
trên mô hình của Volta, Davy đã chế tạo ra pin điện lớn nhất và mạnh
nhất tính đến thời điểm bấy giờ tại tầng hầm của Viện khoa học Hoàng gia
Anh. Những nhân chứng đã kể lại rằng mô hình pin của ông đã làm một
chiếc đèn hồ quang điện chat sáng rực rỡ chưa từng thấy. Ngoài ra, Davy
cũng là người nổi tiếng với việc phát hiện ra khí gây cười N2O hay đèn
mỏ an toàn.
 2 năm sau đó, vào năm 1802, nhà hóa học người Anh, William
Cruickshank thiết kế mô hình pin đầu tiên có thể sản xuất dưới quy mô
công nghiệp. Cruickshank đã đề xuất phương pháp dùng các tấm kẽm và đồng
có cùng kích thước, xếp xen kẽ với nhau, đặt vào một hộp gỗ dài hình
chữ nhật và dán chặt lại. Bên trong hộp có các rãnh để giữ cố định các
tấm kim loại và chứa nước đầy nước muối hoặc acid pha loãng để làm chất
điện phân. Thiết kế này có ưu điểm so với mô hình ban đầu của Volta là
không bị khô và có thể cung cấp được dòng điện mạnh hơn. Mô hình pin của
Cruickshank giống như pin ướt mà chúng ta vẫn còn sử dụng cho đến ngày
nay.
2 năm sau đó, vào năm 1802, nhà hóa học người Anh, William
Cruickshank thiết kế mô hình pin đầu tiên có thể sản xuất dưới quy mô
công nghiệp. Cruickshank đã đề xuất phương pháp dùng các tấm kẽm và đồng
có cùng kích thước, xếp xen kẽ với nhau, đặt vào một hộp gỗ dài hình
chữ nhật và dán chặt lại. Bên trong hộp có các rãnh để giữ cố định các
tấm kim loại và chứa nước đầy nước muối hoặc acid pha loãng để làm chất
điện phân. Thiết kế này có ưu điểm so với mô hình ban đầu của Volta là
không bị khô và có thể cung cấp được dòng điện mạnh hơn. Mô hình pin của
Cruickshank giống như pin ướt mà chúng ta vẫn còn sử dụng cho đến ngày
nay.
Từ pin có thể sạc được, pin ướt cho đến pin khô
 Vào năm 1836, nhà hóa học người Anh, John F. Daniell đã phát triển
một phiên bản pin hoàn thiện hơn với hiệu suất được cải thiện và tạo ra
dòng điện ổn định hơn so với nguyên bản ban đầu của Volta hay
Cruickshank. Tuy nhiên, cho tới thời điểm bấy giờ thì toàn bộ đều là pin
sơ cấp, nghĩa là chỉ dùng được 1 lần và không thể sạc để tái sử dụng
được. Đến năm 1859, nhà vật lý người Pháp Gaston Planté phát minh ra pin
sạc đầu tiên. Đó là một pin với các tấm chì ngăn cách nhau bởi tấm vải
flannel và được đặt trong acid sunfuric loãng. Pin sẽ được sạc lại bằng
cách châm thêm acid vào để tái sử dụng. Mô hình này vẫn còn được sử dụng
cho đến ngày nay dưới tên gọi pin ướt hoặc ắc quy ướt (bình ướt) hoặc
pin carbon zinc
Vào năm 1836, nhà hóa học người Anh, John F. Daniell đã phát triển
một phiên bản pin hoàn thiện hơn với hiệu suất được cải thiện và tạo ra
dòng điện ổn định hơn so với nguyên bản ban đầu của Volta hay
Cruickshank. Tuy nhiên, cho tới thời điểm bấy giờ thì toàn bộ đều là pin
sơ cấp, nghĩa là chỉ dùng được 1 lần và không thể sạc để tái sử dụng
được. Đến năm 1859, nhà vật lý người Pháp Gaston Planté phát minh ra pin
sạc đầu tiên. Đó là một pin với các tấm chì ngăn cách nhau bởi tấm vải
flannel và được đặt trong acid sunfuric loãng. Pin sẽ được sạc lại bằng
cách châm thêm acid vào để tái sử dụng. Mô hình này vẫn còn được sử dụng
cho đến ngày nay dưới tên gọi pin ướt hoặc ắc quy ướt (bình ướt) hoặc
pin carbon zinc

 Năm 1866 tại Pháp, kỹ sư Georges Leclanché (1839-1882) đã chế tạo pin
ướt với các điện cực ngâm mình trong dung dịch điện phân. Tuy nhiên
không lâu sau đó, ông đưa ra sáng kiến cải thiện pin bằng cách dùng dung
dịch hồ amoni chloride sau đó niêm phong pin lại. Sáng kiến này đánh
dấu sự ra đời của thế hệ pin khô. Thế hệ pin mới cho phép pin được sử
dụng ở nhiều vị trí khác nhau, chịu được di chuyển dao động mạnh mà
không sợ dung dịch điện phân bị tràn ra ngoài như pin ướt. Thêm vào đó,
pin cũng được chế tạo thành dạng ống hoặc hình hộp bên trong chứa các bộ
phận khác của pin như các cực dương làm bằng kẽm (anode) và cực âm gồm
mangan dioxide và carbon theo tỷ lệ 8:1 (cathode). Hồ điện cực còn có
thể chứa thêm kẽm chloride.
Năm 1866 tại Pháp, kỹ sư Georges Leclanché (1839-1882) đã chế tạo pin
ướt với các điện cực ngâm mình trong dung dịch điện phân. Tuy nhiên
không lâu sau đó, ông đưa ra sáng kiến cải thiện pin bằng cách dùng dung
dịch hồ amoni chloride sau đó niêm phong pin lại. Sáng kiến này đánh
dấu sự ra đời của thế hệ pin khô. Thế hệ pin mới cho phép pin được sử
dụng ở nhiều vị trí khác nhau, chịu được di chuyển dao động mạnh mà
không sợ dung dịch điện phân bị tràn ra ngoài như pin ướt. Thêm vào đó,
pin cũng được chế tạo thành dạng ống hoặc hình hộp bên trong chứa các bộ
phận khác của pin như các cực dương làm bằng kẽm (anode) và cực âm gồm
mangan dioxide và carbon theo tỷ lệ 8:1 (cathode). Hồ điện cực còn có
thể chứa thêm kẽm chloride.
Năm 1881, Camille Faure chế tạo pin dùng các dải cọc chì oxit làm điện cực để thay thế cho các tấm chì trong pin ướt trước đây. Điều này cho phép tạo ra dòng điện mạnh và ổn định hơn rất nhiều. Đây chính là cơ sở cho sự phát triển của pin ướt sau này với nhiều loại điện cực khác nhau.
 Đến năm 1899, nhà khoa học Waldemar
Jungner đến từ Thụy Điển đã phát minh ra pin nickel-cadimi (NiCd). Đây
là thế hệ pin dùng nickel làm cực âm (cathode) và cadimi làm cực dương
(anode). Tuy nhiên, do chi phí chế tạo khá cao nên pin NiCd không được
áp dụng rộng rãi cho nhiều người sử dụng. 2 năm sau đó, nhà phát minh
nổi tiếng Thomas Edison đã phát triển mô hình pin khác bằng cách dùng
sắt để thay thế Cadimi làm anode giúp giảm giá thành nguyên vật liệu sản
xuất pin. Dù vậy, mô hình pin Nikel-Sắt của Edison đã gặp phải các
nhược điểm nghiêm trọng: năng lượng yếu, hiệu suất kém ở nhiệt độ thấp
và khả năng tự xả cao. Tất cả các nhược điểm trên khiến pin của Edison
cũng không được đưa vào sản xuất và sử dụng rộng rãi.
Đến năm 1899, nhà khoa học Waldemar
Jungner đến từ Thụy Điển đã phát minh ra pin nickel-cadimi (NiCd). Đây
là thế hệ pin dùng nickel làm cực âm (cathode) và cadimi làm cực dương
(anode). Tuy nhiên, do chi phí chế tạo khá cao nên pin NiCd không được
áp dụng rộng rãi cho nhiều người sử dụng. 2 năm sau đó, nhà phát minh
nổi tiếng Thomas Edison đã phát triển mô hình pin khác bằng cách dùng
sắt để thay thế Cadimi làm anode giúp giảm giá thành nguyên vật liệu sản
xuất pin. Dù vậy, mô hình pin Nikel-Sắt của Edison đã gặp phải các
nhược điểm nghiêm trọng: năng lượng yếu, hiệu suất kém ở nhiệt độ thấp
và khả năng tự xả cao. Tất cả các nhược điểm trên khiến pin của Edison
cũng không được đưa vào sản xuất và sử dụng rộng rãi.
Mãi cho tới năm 1932, Shlecht và Ackermann đã đạt được thành công trong việc cải tiến pin NiCd với dòng điện mạnh và tuổi thọ cao. Giải pháp cải tiến của 2 nhà phát minh là trang bị thêm những tấm vách ngăn các điện cực thành nhiều khoang. Năm 1947, George Neumann tiếp tục hoàn thiện mô hình trên thông qua việc chế tạo thế hệ pin NiCd với nhiều vách ngăn bên trong được hàn kín lại.
 Nhiều năm sau đó, pin NiCd tiếp tục là loại pin duy nhất có thể sạc
và di chuyển được. Vào những năm 1990, vấn đề môi trường được quan tâm
hàng đầu tại châu Âu và các nhà khoa học bắt đầu chú ý đến pin NiCd do
khả năng xử lý các hóa chất độc hại sau quá trình sử dụng. Các đạo luật
được ban hành nhằm hạn chế việc sử dụng các nguyên tố này và chuyển sang
sử dụng pin Nickel-Sắt Hydrid (NiMH) thân thiện với môi trường hơn. Dù
vậy, tương tự như pin NiCd, pin NiMH vẫn chưa thật sự đạt được hiệu quả
như mong đợi và các nhà nghiên cứu vẫn tiếp tục phát triển nên một thế
hệ pin ưu việt hơn. Đây chính là bàn đạp tạo tiền đề cho sự ra đời của
pin lithium-ion (Li-ion).
Nhiều năm sau đó, pin NiCd tiếp tục là loại pin duy nhất có thể sạc
và di chuyển được. Vào những năm 1990, vấn đề môi trường được quan tâm
hàng đầu tại châu Âu và các nhà khoa học bắt đầu chú ý đến pin NiCd do
khả năng xử lý các hóa chất độc hại sau quá trình sử dụng. Các đạo luật
được ban hành nhằm hạn chế việc sử dụng các nguyên tố này và chuyển sang
sử dụng pin Nickel-Sắt Hydrid (NiMH) thân thiện với môi trường hơn. Dù
vậy, tương tự như pin NiCd, pin NiMH vẫn chưa thật sự đạt được hiệu quả
như mong đợi và các nhà nghiên cứu vẫn tiếp tục phát triển nên một thế
hệ pin ưu việt hơn. Đây chính là bàn đạp tạo tiền đề cho sự ra đời của
pin lithium-ion (Li-ion).
Pin Li-ion ra đời và phát triển cho đến ngày nay
 Pin Li-ion đầu tiên được đề xuất vào những năm 1970 bởi nhà hóa học
người Mỹ Michael Stanley Whittingham (1941) đến từ Đại học Binghamton sử
dụng titanium sunfide và kim loại liti thuần làm các điện cực. Dù vậy,
do Liti là một kim loại hoạt động mạnh nên khi tiếp xúc với không khí dễ
dàng xảy ra các phản ứng hóa học gây nguy hiểm. Chính vì vậy, mô hình
pin dùng liti thuần làm cực dương đã không được chấp nhận. Cùng thời
gian này, J. O. Besenhard tại Đại học Munich đã phát hiện ra tính chất
trao đổi ion thuận nghịch giữa than chì và cathode bằng oxit kim loại.
Pin Li-ion đầu tiên được đề xuất vào những năm 1970 bởi nhà hóa học
người Mỹ Michael Stanley Whittingham (1941) đến từ Đại học Binghamton sử
dụng titanium sunfide và kim loại liti thuần làm các điện cực. Dù vậy,
do Liti là một kim loại hoạt động mạnh nên khi tiếp xúc với không khí dễ
dàng xảy ra các phản ứng hóa học gây nguy hiểm. Chính vì vậy, mô hình
pin dùng liti thuần làm cực dương đã không được chấp nhận. Cùng thời
gian này, J. O. Besenhard tại Đại học Munich đã phát hiện ra tính chất
trao đổi ion thuận nghịch giữa than chì và cathode bằng oxit kim loại.
Tiếp theo vào năm 1979 tại Đại học Oxford, John Goodenough và Koichi Mizushima đã chế tạo một loại pin sạc tạo ra dòng khoảng 4 V sử dụng Liti Cobalt Oxit (LiCoO2) làm cực dương và liti thuần làm cực âm. LiCoO2 là một chất dẫn điện tích điện dương với tính ổn định cao nên có thể cung cấp các ion liti nhằm tạo ra dòng điện. Khả năng này đã mở ra triển vọng sử dụng LiCoO2 làm cực dương cho các thế hệ pin hoàn toàn mới có thể sạc lại một cách dễ dàng.
Năm 1977, Samar Basu đến từ đại học Pennsylvania đã chứng minh tính khả thi của việc chế tạo và sử dụng pin điện hóa với các điện cực bằng liti và than chì. Không lâu sau đó, mô hình này đã chính thức được chế tạo bởi các kỹ sư tại phòng thí nghiệm Bell (hiện nay là phòng thí nghiệm AT&T).
 Vào năm 1980, Rachid Yazami tiếp tục chứng minh tính điện hóa thuận
nghịch của liti trong than chì. Dù vậy, các chất hữu cơ dùng làm chất
điện phân trong thế hệ pin mới này bị phân hủy trong quá trình sạc. Do
đó, Yazami đã đề xuất hỗn hợp chất hữu cơ rắn bền vững trong quá trình
sạc làm chất điện phân. Mô hình chất điện phân của Yazami vẫn còn sử
dụng trong các thế hệ pin Li-ion cho đến hiện nay.
Vào năm 1980, Rachid Yazami tiếp tục chứng minh tính điện hóa thuận
nghịch của liti trong than chì. Dù vậy, các chất hữu cơ dùng làm chất
điện phân trong thế hệ pin mới này bị phân hủy trong quá trình sạc. Do
đó, Yazami đã đề xuất hỗn hợp chất hữu cơ rắn bền vững trong quá trình
sạc làm chất điện phân. Mô hình chất điện phân của Yazami vẫn còn sử
dụng trong các thế hệ pin Li-ion cho đến hiện nay.
Đến năm 1983, Michael M. Thackeray, Goodnewa và các cộng sự đã xác định có thể dùng khoáng chất Mangan Spinen để chế tạo cực dương cho pin Li-ion. Đây là loại khoáng chất có tính dẫn điện tốt, giá thành rẻ và hoạt động ổn định. Tuy vẫn còn nhược điểm là bị tiêu hao dần trong quá trình sạc nhưng vẫn có thể khắc phục bằng các biện pháp chỉnh sửa hóa học. Cho đến năm 2013, Mangan Spinen vẫn tiếp tục được sử dụng cho các thế hệ pin Li-ion thương mại.
 Vào năm 1985, Akira Yoshino lắp ráp mô hình pin đầu tiên dựa trên tất
cả các yếu tố thành công từ trước, sử dụng vậy liệu cacbonate giúp giữ
các ion liti trong 1 điện cực giúp LiCoO2 bền vững trong không khí hơn.
Chính vì lý do này, thế hệ pin Li-ion đã được hoàn thiện và an toàn hơn
rất nhiều so với trước đây.
Vào năm 1985, Akira Yoshino lắp ráp mô hình pin đầu tiên dựa trên tất
cả các yếu tố thành công từ trước, sử dụng vậy liệu cacbonate giúp giữ
các ion liti trong 1 điện cực giúp LiCoO2 bền vững trong không khí hơn.
Chính vì lý do này, thế hệ pin Li-ion đã được hoàn thiện và an toàn hơn
rất nhiều so với trước đây.
 Năm 1991, tập đoàn điện tử Sony chính thức thương mại hóa pin Li-ion
dưới quy mô sản xuất công nghiệp. Cho đến nay, hầu hết các hoạt động
nghiên cứu đều xoay quanh việc cải thiện hiệu suất của pin Li-on. Bên
cạnh việc cung cấp năng lượng cho điện thoại di động, máy tính xách tay,
máy ảnh kỹ thuật số, dụng cụ điện và các thiết bị y tế, pin Li-ion hiện
nay còn được sử dụng cho xe điện. Đây là thế hệ pin đáng chú ý nhất
tính đến thời điểm hiện tại do có mức lưu trữ năng lượng cụ thể, thiết
kế đơn giản, hiệu suất cao, cho dòng ổn định, chi phí bảo trì thấp và
khá thân thiện với môi trường.
Năm 1991, tập đoàn điện tử Sony chính thức thương mại hóa pin Li-ion
dưới quy mô sản xuất công nghiệp. Cho đến nay, hầu hết các hoạt động
nghiên cứu đều xoay quanh việc cải thiện hiệu suất của pin Li-on. Bên
cạnh việc cung cấp năng lượng cho điện thoại di động, máy tính xách tay,
máy ảnh kỹ thuật số, dụng cụ điện và các thiết bị y tế, pin Li-ion hiện
nay còn được sử dụng cho xe điện. Đây là thế hệ pin đáng chú ý nhất
tính đến thời điểm hiện tại do có mức lưu trữ năng lượng cụ thể, thiết
kế đơn giản, hiệu suất cao, cho dòng ổn định, chi phí bảo trì thấp và
khá thân thiện với môi trường.
Tiếp theo đó là sự kiện công ty Bellcore chính thức thương mại hóa pin Li-ion Polymer vào năm 1994 sau quá trình nghiên cứu. Bước tiếp theo là pin sự xuất hiện của pin li-ion với cathode bằng mangan, pin li-phosphate được các nhà khoa học liên tục cải tiến và hoàn thiện để chính thức thương mại hóa. Các nhà khoa học dự đoán tiếp theo sẽ là sự ra đời của những thế hệ pin phát triển dựa trên tiến bộ của công nghệ nano giúp tăng cường hiệu suất cũng như kích thước và tuổi thọ của pin.
Tóm tắt các cột mốc quan trọng có liên quan mật thiết đến quá trình phát triển của pin
Một trong những phát minh vĩ đại và đáng chú ý nhất của con người trong 400 năm qua chính là điện. Những dòng điện đầu tiên có thể được tạo ra trước đó, nhưng mãi đến cuối những năm 1800 thì nhân loại mới chứng kiến được những ứng dụng cụ thể của điện. Đó là 250.000 bóng đèn dây tóc thắp sáng Triễn lãm tiêu dùng tại Chicago, Mỹ năm 1893 hay làm một cây cầu bắt qua sông Seine, Paris phát sáng tại Hội chợ thế giới năm 1900.
Tuy nhiên, những dòng điện đầu tiên đã được con người tạo ra từ nhiều năm trước đó. Vào năm 1963, trong quá trình xây dựng tuyến đường sắt gần Baghdad, những công nhân đã phát hiện ra những "viên pin của người Parthian" có niên đại lên tới 2000 năm nằm trong một hầm mộ cổ. Đây là những viên pin xuất hiện sớm nhất trong lịch sử loài người do bàn tay chế tạo của những người Parthian, một dân tộc miền Bắc Ba Tư.
Qua đó, các nhà khoa học đã dự đoán rằng những người Parthian cổ đại đã sử dụng các công cụ tạo ra dòng điện để mạ vàng và bạc vào những vật dụng từ những năm 250 trước công nguyên. Nhiều nhà khoa học cho rằng người Parthian chỉ sử dụng các công cụ trên cho mục đích mạ chứ chưa nhìn nhận nó như một nguồn năng lượng. Nhiều bằng chứng khảo cổ khác cho thấy những người Ai Cập cổ đại cũng đã biết mạ antimon lên các vật dụng bằng đồng từ hơn 4300 năm trước. Các di tích khảo cổ khác cũng cho thấy những người Babylon cũng đã khám phá và sử dụng kỹ thuật dùng nước ép nho như một chất điện phân để mạ vàng lên đồ trang sức.
1786 - Cặp chân nhái đã chết nhưng biết cử động!
giáo
sư Cơ thể học Luigi Galvani (1737-1798) với phát hiện đâm que sắt vào
chân nhái đặt trên bàn kim loại khiến chân nhái co giật
Một ngày khác, Galvani đã dùng một móc đồng phơi đôi chân nhái phía trên một thanh sắt ngoài ban công. Galvani đã nhận thấy rằng khi gió thổi khiến đôi chân nhái đung đưa chạm vào thanh sắt và ngay tức khắc, chân nhái sẽ bị co giật. Ông suy nghĩ để cố lý giải cho hiện tượng kỳ lạ này và một ý tưởng đã lóe lên trong đầu ông: điện. Galvani kết luận rằng điện có trong khắp mọi vật và có trong cả đôi chân nhái. Ông đặt tên cho loại điện này là "điện của sinh vật" và công bố phát hiện của mình trên một bài báo khiến cho giới khoa học gia châu Âu hết sức sửng sốt với loại điện mới này.
Ngày nay, chúng ta đều biết rằng Galvani đã nhầm lẫn khi cho rằng đó là điện của sinh vật và ông chỉ dừng lại ở hiện tượng mà không tìm hiểu nguyên nhân sinh ra điện. Tuy nhiên, phát hiện trên của Galvani đã tiến rất gần tới những nguyên lý mở đường cho việc chế tạo pin sau này.
"Pin Volta" - Pin đầu tiên của nhân loại ra đời vào năm 1800
Alessandro Volta (1745-1827) là giáo sư vật lý tại Đại học Pavie, Italy, cha đẻ của pin
Từ khi Galvani phổ biến các phát hiện của mình về "điện của sinh vật" vào năm 1791, tại nhiều phòng thí nghiệm lớn tại châu Âu, hàng loạt các nhà khoa học đã thực hiện các thí nghiệm với đôi chân nhái của Galvani. Có người đã nối đôi chân nhái với chai Leiden (hình thái đầu tiên của tụ điện, một chai thủy tinh tích trữ tĩnh điện giữa 2 điện cực bên trong và bên ngoài chai) và nhận thấy rằng đôi chân nhái có sự co giật dữ dội. Với thí nghiệm trên, các nhà khoa học bắt đầu nghi ngờ về giả thuyết "điện sinh vật" của Galvani. Trong số những người phản đối giả thuyết có Alessandro Volta.
Đối với thí nghiệm chân nhái , Volta không quan tâm đến hiện tượng co giật đơn thuần, sâu xa hơn, ông cố gắng tìm hiểu nguồn điện đã sinh ra từ đâu để làm chân nhái có thể co giật. Volta nhận thấy rằng chân nhái chỉ co giật khi có sự tiếp xúc của 2 kim loại khác nhau. Sau khi tiếp tục nghiên cứu, Volta phát hiện thêm rằng điện sinh ra do phản ứng hóa học và hiện tượng co giật của chân ếch chỉ xảy ra khi 2 kim loại khác nhau tiếp xúc trong một dung dịch muối. Cụ thể, dung dịch muối tồn tại bên trong cơ thịt của chân nhái.
Mô hình pin của Volta
Mô hình pin đầu tiên của Volta còn được bảo tồn đến ngày nay
Hình ảnh Volta đang thực hiện thí nghiệm với sự theo dõi trực tiếp của hoàng đế nước Pháp Napoleon Bonaparte.
Nhà vật lý và hóa học người Cornwall, vương quốc Anh, Humphry Davy (1778-1829) cùng mô hình pin.
Nhà hóa học người Anh, William Cruickshank với thiết kế mô hình pin đầu tiên có thể sản xuất dưới quy mô công nghiệp
Từ pin có thể sạc được, pin ướt cho đến pin khô
Pin ướt có thể sạc được của nhà vật lý người Pháp Gaston Planté
Kỹ sư người Pháp Georges Leclanché (1839-1882) và mô hình pin của ông.
Năm 1881, Camille Faure chế tạo pin dùng các dải cọc chì oxit làm điện cực để thay thế cho các tấm chì trong pin ướt trước đây. Điều này cho phép tạo ra dòng điện mạnh và ổn định hơn rất nhiều. Đây chính là cơ sở cho sự phát triển của pin ướt sau này với nhiều loại điện cực khác nhau.
Pin NiCd
Mãi cho tới năm 1932, Shlecht và Ackermann đã đạt được thành công trong việc cải tiến pin NiCd với dòng điện mạnh và tuổi thọ cao. Giải pháp cải tiến của 2 nhà phát minh là trang bị thêm những tấm vách ngăn các điện cực thành nhiều khoang. Năm 1947, George Neumann tiếp tục hoàn thiện mô hình trên thông qua việc chế tạo thế hệ pin NiCd với nhiều vách ngăn bên trong được hàn kín lại.
Pin NiMH quen thuộc với tất cả chúng ta ngày nay
Pin Li-ion ra đời và phát triển cho đến ngày nay
Nhà hóa học người Mỹ Michael Stanley Whittingham, người đầu tiên đề xuất ý tưởng pin Li-ion
Tiếp theo vào năm 1979 tại Đại học Oxford, John Goodenough và Koichi Mizushima đã chế tạo một loại pin sạc tạo ra dòng khoảng 4 V sử dụng Liti Cobalt Oxit (LiCoO2) làm cực dương và liti thuần làm cực âm. LiCoO2 là một chất dẫn điện tích điện dương với tính ổn định cao nên có thể cung cấp các ion liti nhằm tạo ra dòng điện. Khả năng này đã mở ra triển vọng sử dụng LiCoO2 làm cực dương cho các thế hệ pin hoàn toàn mới có thể sạc lại một cách dễ dàng.
Năm 1977, Samar Basu đến từ đại học Pennsylvania đã chứng minh tính khả thi của việc chế tạo và sử dụng pin điện hóa với các điện cực bằng liti và than chì. Không lâu sau đó, mô hình này đã chính thức được chế tạo bởi các kỹ sư tại phòng thí nghiệm Bell (hiện nay là phòng thí nghiệm AT&T).
Rachid Yazami, người chứng minh tính điện hóa thuận nghịch của liti trong than chì
Đến năm 1983, Michael M. Thackeray, Goodnewa và các cộng sự đã xác định có thể dùng khoáng chất Mangan Spinen để chế tạo cực dương cho pin Li-ion. Đây là loại khoáng chất có tính dẫn điện tốt, giá thành rẻ và hoạt động ổn định. Tuy vẫn còn nhược điểm là bị tiêu hao dần trong quá trình sạc nhưng vẫn có thể khắc phục bằng các biện pháp chỉnh sửa hóa học. Cho đến năm 2013, Mangan Spinen vẫn tiếp tục được sử dụng cho các thế hệ pin Li-ion thương mại.
Sơ đồ nguyên lý hoạt động của pin Li-ion
Viên pin Li-ion này có quen thuộc với các bạn không?
Tiếp theo đó là sự kiện công ty Bellcore chính thức thương mại hóa pin Li-ion Polymer vào năm 1994 sau quá trình nghiên cứu. Bước tiếp theo là pin sự xuất hiện của pin li-ion với cathode bằng mangan, pin li-phosphate được các nhà khoa học liên tục cải tiến và hoàn thiện để chính thức thương mại hóa. Các nhà khoa học dự đoán tiếp theo sẽ là sự ra đời của những thế hệ pin phát triển dựa trên tiến bộ của công nghệ nano giúp tăng cường hiệu suất cũng như kích thước và tuổi thọ của pin.
Theo Tinhte



Nhận xét
Đăng nhận xét