CÁC BẬC NHÂN TÀI KHOA HỌC 32

(ĐC sưu tầm trên NET)

94

Louis de Broglie: Người đưa ra khái niệm "sóng vật chất" Viết bởi Huỳnh Vĩnh Phát Thứ ba, 20 Tháng 3 2012 12:30 Louis Victor Pierre Raymond, 7th duc de Broglie, FRS (sinh tại Dieppe, Pháp vào ngày 15 tháng 8 năm 1892 – mất tại Louveciennes, Pháp, ngày 19 tháng 3 năm 1987) là một nhà vật lý Pháp. Ông là thành viên thứ 16 được bầu vào vị trí số 1 của Académie française năm 1944 và là thư ký vĩnh viễn của Viện hàn lâm khoa học Pháp. Ông đoạt Giải Nobel Vật lý năm 1929. Louis de Broglie Cuộc đời Louis de Broglie sinh ra trong một gia đình quý tộc ở Dieppe, Seine-Maritime, con trai thứ của Victor, đệ ngũ công tước của Broglie. Ông trở thành đệ thất công tước Broglie sau khi người anh trai không có người thừa kế qua đời vào năm 1960, Maurice, đệ lục công tước của Broglie, cũng là một nhà vật lý. Ông không kết hôn. Khi ông qua đời ở Louveciennes, ông đã được kế vị tước công tước một họ hàng xa, Victor-François, đệ bát công tước của Broglie. De Broglie đã dự định theo nghề khoa học nhân văn, và nhận được bằng đầu tiên ngành lịch sử. Sau đó, mặc dù ông đã chuyển sự chú ý của ông đối với toán học và vật lý và tốt nghiệp vật lý. Với sự bùng nổ của thế chiến thứ nhất vào năm 1914, ông gia nhập quân ngũ và tham gia vào việc phát triển thông tin vô tuyến. Nghiên cứu năm 1924 của ông Recherches sur la théorie des quanta (nghiên cứu về lý thuyết lượng tử), giới thiệu lý thuyết của ông về sóng điện tử. Điều này bao gồm thuyết vật chất nhị nguyên sóng-hạt, dựa trên công việc của Max Planck và Albert Einstein về ánh sáng. Các giám khảo luận án, không chắc chắn của luận án, đã chuyển luận văn cho Einstein để đánh giá và Einstein đã hoàn toàn tán thành đề xuất tính nhị nguyên sóng-hạt của ông, De Broglie đã được trao bằng tiến sĩ. Nghiên cứu này lên đến đỉnh điểm trong giả thuyết de Broglie nói rằng bất kỳ hạt di chuyển của hạt hoặc của vật thểt đều có một sóng liên quan. De Broglie do đó tạo ra một lĩnh vực mới trong vật lý, ondulatoire mécanique, hoặc cơ học sóng, kết hợp vật lý năng lượng (sóng) và vấn đề (hạt). Do đóng góp này, ông đã đoạt giải Nobel Vật lý năm 1929. Giả thuyết De Broglie Khi nghiên cứu mẫu nguyên tử của Bohr, De Broglie nảy ra ý tưởng rằng không nên chỉ coi electron là một hạt mà có thể gán cho nó một tính tuần hoàn nào đó. Ông nêu vấn đề: nếu trong lý thuyết về ánh sáng suốt một thế kỷ trước đó người ta đã coi nhẹ khái niệm "hạt", chỉ sử dụng khái niệm "sóng", thì trong lý thuyết về vật chất người ta có phạm sai lầm ngược lại không? Có xem nhẹ khái niệm sóng và chỉ sử dụng khái niệm hạt không? Và ông sửa chữa sai lầm đó bằng cách nêu lên khái niệm "sóng vật chất". Như ta đã biết ánh sáng vừa có tính chất sóng vừa có tính chất hạt. Tính chất sóng thể hiện ở hiện tượng giao thoa, nhiễu xạ v.v…, còn tính chất hạt thể hiện trong các hiện tượng quang điện, compton v.v… Lưỡng tính sóng hạt được Einstein nêu lên trong thuyết lượng tử ánh sáng. Theo thuyết này ánh sáng được cấu tạo bởi các hạt photon và: Từ hai công thức  ta thấy rõ: những đại lượng đặc trưng cho tính chất hạt (E, p), những đại lượng đặc trưng cho tính chất sóng (λ, f) của ánh sáng liên hệ chặt chẽ với nhau. Do ánh sáng và các chất đều là các dạng năng lượng có thể chuyển hóa cho nhau, nên De Broglie cho rằng các chất cũng có tính chất lưỡng tính và các hạt như: electron và sau đó đối mọi vi hạt khác cũng có tính chất sóng hạt. Nếu áp dụng hệ thức trên cho các electron và nói chung cho các hạt vật chất có khối lượng m và vận tốc v ta cũng có thể nói rằng mỗi hạt vật chất đều có bước sóng và tần số là: Chú ý rằng : Vì sóng này không phải là sóng điện từ. Bước sóng đó sau này được gọi là bước sóng De Broglie của hạt. Bản thân De Broglie và các nhà vật lý khác lúc đó không xác định được bản chất của sóng đó là gì. De Broglie chứng minh được rằng khi electron chuyển động trên một quỹ đạo khép kín với một vận tốc không đổi v << c thì quỹ đạo đó là bền nếu nó chứa một số nguyên các bước sóng De Broglie của electron. Điều đó phù hợp với các phép tính toán của Bohr đối với mẫu nguyên tử của Bohr. De Broglie cũng nêu lên rằng nếu cho một chùm electron đi qua một khe rất nhỏ thì có thể quan sát được sự nhiễu xạ của electron. Tức là sự thể hiện tính sóng của electron. Đó là sự kiểm tra lý thuyết của ông bằng thực nghiệm.  Năm 1927, sự nhiễu xạ của electron đã được phát hiện một cách tình cơ. Năm 1929, De Broglie được nhận giải thưởng Nobel.  Ý tưởng về sóng vật chất là một ý tưởng rất kỳ lạ. Nếu như ý tường về lượng tử năng lượng, về hạt ánh sáng nảy sinh do nhu cầu phải giải thích một số hiện tượng cụ thể, thì lúc đó không có sự kiện thực nghiệm nào đặt ra yêu cầu phải nảy sinh ý tưởng về sóng vật chất.  Ý tưởng đó nảy ra do tư duy rất tinh tế của De Broglie, và ông đã đưa nó vào luận án tiến sĩ mà ông bảo vệ năm 1924. Einstein đã khuyên một học trò của mình đọc kỷ luận án này. Einstein nói: "Nó giống như bài viết của một gã điên rồ, nhưng lập luận thì rất vững vàng." Ý tưởng của De Broglie đã gây ấn tượng mạnh mẽ đến Schrödinger, và trên cơ sở đó Schrödinger xây dựng nên phương trình Schrödinger nổi tiếng ... Nội dung giả thuyết De Broglie Một vi hạt tự do có năng lượng xác định, động lượng xác định tương ứng với một sóng phẳng đơn sắc xác định: Năng lượng của vi hạt liên hệ với tần số dao động của sóng tương ứng theo hệ thức: Động lượng của vi hạt liên hệ với bước sóng theo hệ thức: Sóng De Broglie là sóng vật chất, sóng của các vi hạt. Điền Quang – Thuvienvatly.com Tài liệu tham khảo: Wikipedia Lịch sử Vật Lý - Đào văn Phúc Lịch sử Vật Lý - Nguyễn Thị Thiếp Giáo trình Vật Lý A2 Vui lòng ghi rõ "Nguồn Thuvienvatly.com" khi đăng lại bài từ CTV của chúng tôi.

Louis-Victor de Broglie 1892-1987 Pháp Vật Lý

95

Bộ đếm Geiger-Müller Đồng vị Thori Urani Bách khoa toàn thư mở Wikipedia Một bộ đếm Geiger-Müller Bộ đếm Geiger–Müller, hay còn được goi là Bộ đếm Geiger là phát minh của hai nhà vật lý người Đức Hans Geiger và Walther Müller. Đây là một thiết bị rất hữu ích, bởi nó giúp các nhà khoa học phát hiện ra tia gamma, hạt alpha, hạt beta và các dạng khác của bức xạ ion hóa. Bộ đếm này được dùng để phát hiện ra các nguyên tố phóng xạ như urani, thori. Nó cũng được dùng trong các công việc có liên quan đến đồng vị phóng xạ.

Hans Geiger 1883-1945 Đức Vật Lý

9 Thuyết địa tâm liệu có sai? Hoa Hướng Dương | 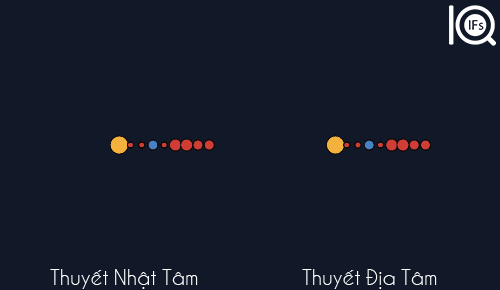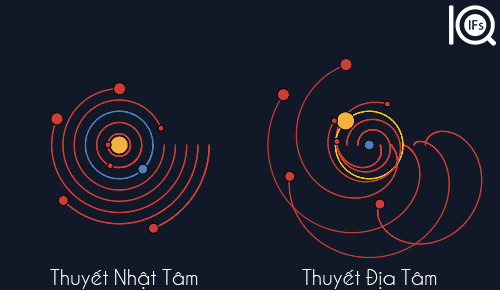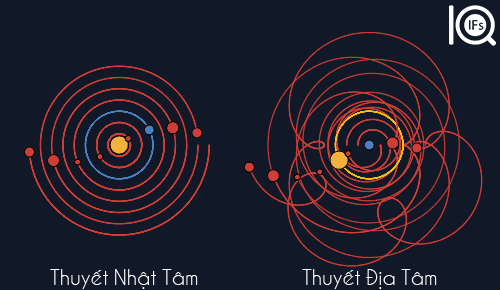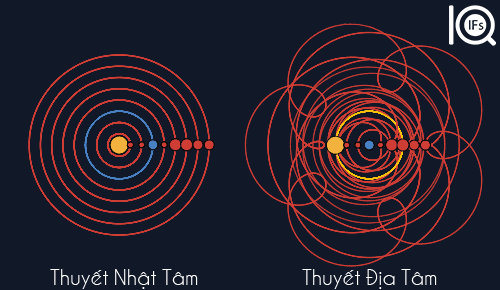11/01/2016 20:15 8 Quỹ đạo của hệ Nhật tâm rõ ràng dễ khảo sát hơn rất nhiều Trong thiên văn học, thuyết địa tâm của vũ trụ là lý thuyết cho rằng Trái Đất là trung tâm của vũ trụ và Mặt Trời cùng các thiên thể khác quay quanh nó. 1. Học thuyết Địa tâm của Ptolemy Thuyết Địa tâm của Ptolemy Hệ này được coi là hình mẫu tiêu chuẩn thời Hy Lạp cổ đại, được cả Aristotle và Ptolemy, cũng như đa số các nhà triết học Hy Lạp đồng thuận rằng: Mặt Trời, Mặt Trăng, các ngôi sao và những hành tinh (có thể quan sát được bằng mắt thường) đều quay quanh Trái Đất. Mô hình địa tâm là quan điểm thống trị thời tiền hiện đại; từ cuối thế kỷ 16 trở về sau nó dần bị thay thế bởi Hệ Nhật tâm của Copernicus, Galileo và Kepler. Các hành tinh và Mặt trời quay quanh Trái đất Trong hệ Ptolemy, mỗi hành tinh chuyển động trên hai hay nhiều mặt cầu: Một mặt cầu chính với tâm là Trái Đất, và các mặt cầu khác được gọi là ngoại luân nằm trên mặt cầu chính. Hành tinh chuyển động trên các mặt cầu và ngoại luân đó. Các mặt cầu ngoại luân Mặt cầu chính quay quanh Trái Đất trong khi ngoại luân quay bên trong mặt cầu chính, khiến hành tinh có thể tiến gần hay rời xa Trái Đất hơn, tùy theo các điểm khác nhau trên quỹ đạo của nó, và thậm chí có thể di chuyển chậm, dừng lại, đi giật lùi . Các ngoại luân của Sao Kim và Sao Thủy luôn có tâm trên một đường thẳng nối Trái Đất với Mặt trời (Sao Thủy gần Trái Đất hơn), điều này giải thích tại sao chúng luôn gần nhau trên bầu trời. Thứ tự các hành tinh từ Trái Đất trở ra theo hệ Ptolemy như sau: Mặt Trăng, Sao Thủy, Sao Kim, Mặt trời, Sao Hỏa, Sao Mộc Thổ, các định tinh... Không may thay, hệ này ở thời Ptolemy không tương thích lắm với các quan sát, thậm chí khi nó đã được cải tiến nhiều so với hệ Aristotle. Thỉnh thoảng kích thước các hành tinh đang thụt lùi nhỏ lại, và thỉnh thoảng lại to hơn. Quan điểm Trái đất là tâm vũ trụ được nhà Thờ ủng hộ Hệ thống cuối cùng được nhiều người chấp nhận ở phương tây là một hệ thống rất cồng kềnh khi quan sát theo quan điểm hiện nay. Mỗi hành tinh cần một ngoại luân quay quanh mặt cầu chính, được bù thêm bằng một tâm sai khác nhau tùy theo hành tinh. Nhưng hệ này lại phán đoán được chuyển động của nhiều thiên thể, gồm cả sự khởi đầu và kết thúc của chuyển động lùi, khá chính xác ở thời điểm ấy. 2. Thuyết Nhật Tâm của Copernicus Copernicus Năm 1543, hệ địa tâm lần đầu tiên bị thách thức nghiêm trọng khi Copernicus xuất bản cuốn Về chuyển động quay của các thiên thể, ấn định rằng Trái Đất và các hành tinh khác đều quay quanh Mặt trời. Với sự phát minh ra kính viễn vọng năm 1609, những cuộc quan sát đầu tiên do Galileo tiến hành (như Sao Thổ có các Mặt Trăng) đặt ra một số nghi vấn đối với những giáo lý của thuyết địa tâm nhưng không đe dọa nghiêm trọng tới vị trí của nó. Quan điểm Copernicus chống lại nhà Thờ Hệ địa tâm vẫn còn tồn tại nhiều năm sau đó, bởi vì ở thời ấy hệ Copernicus không đưa ra được các tiên đoán tốt hơn về vị trí các hành tinh so với hệ địa tâm, và nó đặt ra các vấn đề đối với cả triết học tự nhiên và Kinh thánh. 3. Hệ quy chiếu Mọi thứ đều là tương đối dựa vào hệ quy chiếu Như chúng ta đã biết, mọi chuyển động và đứng yên đều là tương đối, tùy vào hệ quy chiếu. Ví dụ, trong hệ quy chiếu Trái Đất thì Trái Đất đứng yên, Mặt Trời chuyển động, còn bề mặt trái đất thì phẳng lì. Nhưng trong hệ quy chiếu Hệ Mặt Trời thì Mặt Trời đứng yên, Trái Đất chuyển động, bề mặt Trái Đất hình cầu. Đến hệ quy chiếu ngân hà, Mặt Trời chuyển động. Vì mọi chuyển động và đứng yên mà chúng ta thấy hầu như là ảo hết. Hệ mặt trời Trong cách thức tính toán hiện đại, gốc và hướng của một hệ tọa độ thường phải được lựa chọn. Vì các lý do thực tiễn, các hệ tọa độ có gốc tại trung tâm khối lượng Trái Đất, khối lượng Mặt Trời hay trung tâm khối lượng của Hệ Mặt Trời thường được sử dụng. Tính từ "địa tâm" hay "nhật tâm" có thể được sử dụng trong ngữ cảnh này. Tuy nhiên, sự lựa chọn các hệ tọa độ như vậy không hề có những liên quan triết học hay vật lý. Quỹ dạo theo tâm là Mặt trời Fred Hoyle (1915-2001) là nhà thiên văn học người Anh từng viết: "Mối quan hệ giữa hai mô hình địa tâm và nhật tâm được đơn giản hóa thành một sự chuyển đổi hệ tọa độ bình thường và đó chính là nguyên tắc cơ bản lý thuyết của Einstein cho rằng: Bất kỳ hai cách tiếp cận nào đối với thế giới có quan hệ với nhau bởi một sự chuyển đổi hệ quy chiếu thì hoàn toàn tương tự với nhau từ quan điểm vật lý." Từ quan điểm khoa học hiện đại, đặc biệt theo thuyết tương đối rộng của Einstein, không hề có hệ tham chiếu tuyệt đối, mà chỉ có những hệ tham chiếu thích hợp hay không thích hợp cho một mục đích quan sát mà thôi. Một hệ tham chiếu với Trái Đất là trung tâm thích hợp cho những hoạt động thường ngày và đa số các thực nghiệm khác, nhưng nó lại không phải là một lựa chọn tốt cho cơ học hệ mặt trời và du lịch không gian. Trong khi hệ tham chiếu với mặt trời ở trung tâm thích hợp hơn cho những trường hợp đó, thiên văn học thiên hà và ngoại thiên hà dễ tiếp cận hơn nếu coi Mặt trời không đứng yên cũng không phải là trung tâm vũ trụ mà đang quay quanh trung tâm ngân hà. Mô hình địa tâm (Ptolemy) về hệ mặt trời vẫn thường được những người chế tạo các mô hình thiên văn học ưa chuộng, bởi vì, về lý do kỹ thuật, cơ cấu chuyển động của các hành tinh kiểu Ptolemy có nhiều ưu thế hơn so với hệ Copernicus. Những người tiên phong của thuyết Nhật tâm Các mặt cầu thiên thể, được sử dụng cho các mục đích giảng dạy và thỉnh thoảng cho cả mục đích hoa tiêu cũng vẫn dựa trên hệ địa tâm. Như vậy ý tưởng Địa tâm hay Nhật tâm hay thâm chí lấy bất cứ hành tinh nào trong hệ mặt trời làm tâm của hệ quy chiếu đều đúng. Vấn đề chỉ là nó có phù hợp hay thuận tiện với việc quan sát và tính toán của con người hay không mà thôi. Khó tin: Đường thẳng không phải là con đường nhanh nhất! theo Trí Thức Trẻ Ptolemy Một trong những ảnh hưởng nhất nhà thiên văn học Hy Lạp và địa lý thời gian của mình, Ptolemy propounded lý thuyết địa tâm trong một hình thức mà thắng cho năm 1400. Tuy nhiên, tất cả các nhà toán học Hy Lạp cổ đại, nó là công bằng để nói rằng công việc của mình đã tạo ra thảo luận và tranh luận nhiều hơn bất kỳ khác. Chúng ta sẽ thảo luận về các đối số cho dưới đây, tùy thuộc vào đó là chính xác, họ vai Ptolemy trong đèn rất khác nhau. Các đối số của một số nhà sử học cho thấy rằng Ptolemy là một nhà toán học của các cấp bậc rất cao nhất, lập luận của những người khác chỉ ra rằng ông không có nhiều hơn một expositor tuyệt vời, nhưng đến nay tồi tệ hơn, một số yêu cầu bồi thường thậm chí rằng ông cam kết một tội ác chống lại các nhà khoa học đồng bào của mình bằng cách phản bội các đạo đức nghề nghiệp và tính toàn vẹn của mình. Chúng tôi biết rất ít về cuộc sống của Ptolemy. Ông đã quan sát thiên văn từ Alexandria ở Ai Cập trong những năm AD 127-41. Trong thực tế, quan sát ngày đầu tiên mà chúng tôi có thể chính xác đã được thực hiện bởi Ptolemy ngày 26 tháng 3, trong khi 127 cuối cùng đã được thực hiện vào ngày 02 Tháng 2 141. Đó là tuyên bố của Theodore Meliteniotes trong khoảng 1360 là Ptolemy được sinh ra ở Hermiou (mà là ở Thượng Ai Cập hơn là Hạ Ai Cập, nơi Alexandria nằm) nhưng kể từ khi tuyên bố này lần đầu tiên xuất hiện nhiều hơn một ngàn năm sau khi Ptolemy sống, nó phải được coi như là tương đối không đúng. Trong thực tế, không có bằng chứng rằng Ptolemy đã bao giờ hết bất cứ nơi nào khác hơn là Alexandria. Tên của ông, Claudius Ptolemy, tất nhiên là một hỗn hợp của Ai Cập Hy Lạp 'Ptolemy' và La Mã 'Claudius. Điều này sẽ cho thấy ông là hậu duệ của một cuộc sống gia đình Hy Lạp tại Ai Cập và rằng ông là một công dân của Rome, trong đó sẽ là kết quả của một hoàng đế La Mã cho rằng phần thưởng '' đến một trong những tổ tiên Ptolemy. Chúng tôi biết rằng các quan sát Ptolemy được sử dụng do 'Theon các nhà toán học', và điều này đã gần như chắc chắn Theon của Smyrna người gần như chắc chắn là cô giáo của mình. Chắc chắn điều này sẽ làm cho tinh thần kể từ Theon được cả một người quan sát và một nhà toán học người đã viết về các chủ đề như: Liên từ thiên văn, eclipses, Occultations và quá cảnh. Hầu hết các công trình đầu Ptolemy Syrus được dành riêng cho những người có thể cũng đã được một trong những giáo viên của ông ở Alexandria, nhưng không có gì là nổi tiếng của Syrus. Nếu những dữ kiện về giáo viên Ptolemy là đúng thì chắc chắn trong Theon ông không có một học giả lớn, cho Theon dường như không có hiểu sâu bất kỳ công việc thiên văn ông mô tả. Mặt khác Alexandria đã có một truyền thống cho học bổng này sẽ có nghĩa là ngay cả khi Ptolemy đã không được tiếp cận với các giáo viên tốt nhất, ông sẽ có quyền truy cập vào các thư viện, nơi ông đã có thể tìm thấy các tài liệu tham khảo có giá trị mà ông đã sử dụng tốt. Ptolemy công trình lớn đã tồn tại và chúng ta sẽ thảo luận về chúng trong bài viết này. Điều quan trọng nhất, tuy nhiên, là Almagest luận đó là một trong mười ba cuốn sách. Chúng ta nên nói ngay rằng, mặc dù việc này là bây giờ hầu như luôn luôn được biết đến như Almagest đó không phải tên gốc của nó. Tiêu đề bản gốc tiếng Hy Lạp của nó dịch là Những biên tập Toán học nhưng tiêu đề này nhanh chóng được thay thế bằng một tên Hy Lạp có nghĩa là The Greatest biên tập. Này đã được dịch sang tiếng Ả Rập là "al-majisti" và từ này tiêu đề Almagest đã được trao cho các công việc khi nó được dịch từ tiếng Ả Rập để Latin. Almagest là sớm nhất của Ptolemy công trình và cho chi tiết các lý thuyết toán học của các chuyển động của Mặt Trời, Mặt Trăng, và các hành tinh. Ptolemy nhiều đóng góp của mình bằng việc đưa bản gốc hầu hết các chi tiết cho các chuyển động của mỗi của các hành tinh. Các Almagest đã không được thay thế cho đến khi một thế kỷ sau khi Copernicus trình bày lý thuyết nhật tâm của mình trong revolutionibus De của 1543. Grasshoff viết trong: Ptolemy "Almagest" cổ phiếu với Euclid 's "Elements" vinh quang của khoa học đang được các văn bản dài nhất trong sử dụng. Từ quan niệm của mình trong thế kỷ thứ hai cho đến cuối thời Phục Hưng, công tác này được xác định thiên văn học là một khoa học. Trong thời gian này các "Almagest" không chỉ là một công việc về thiên văn học; đề đã được định nghĩa là những gì được mô tả trong "Almagest". Ptolemy mô tả mình rất rõ ràng những gì anh ta cố gắng làm bằng văn bản cho công việc (xem ví dụ): Chúng tôi sẽ cố gắng ghi xuống tất cả mọi thứ mà chúng tôi nghĩ rằng chúng tôi đã phát hiện cho đến thời điểm hiện nay, chúng ta phải làm điều này là ngắn gọn càng tốt và một cách có thể được theo sau bởi những người đã thực hiện một số tiến bộ trong lĩnh vực này. Vì lợi ích của sự hoàn chỉnh trong việc điều trị của chúng tôi, chúng tôi sẽ đưa ra tất cả những gì hữu ích cho các lý thuyết của trời theo thứ tự đúng, nhưng để tránh dài quá đáng, chúng tôi chỉ đơn thuần là trách nhiệm recount đầy đủ những gì đã được thành lập bởi các Ancients. Tuy nhiên, những chủ đề đó chưa được xử lý bằng tiền nhiệm của chúng tôi tại tất cả, hay là không hữu ích như họ có thể có được, sẽ được thảo luận tại chiều dài đến khả năng tốt nhất của chúng tôi. Ptolemy đầu tiên của tất cả các biện minh cho ông mô tả của vũ trụ dựa trên trái đất làm trung tâm hệ thống mô tả của Aristotle. Nó là một cái nhìn của thế giới dựa trên một khoảng đất cố định mà mặt cầu của những ngôi sao cố định quay mỗi ngày, điều này thực hiện với nó trong lĩnh vực của mặt trời, mặt trăng, và các hành tinh. Ptolemy được sử dụng các mô hình hình học để dự đoán các vị trí của mặt trời, mặt trăng, và các hành tinh, sử dụng các kết hợp của các chuyển động tròn được gọi là ngoại luân. Có thiết lập mô hình này, Ptolemy sau đó đi vào để mô tả toán học mà ông cần trong phần còn lại của tác phẩm. Đặc biệt, ông giới thiệu phương pháp trigonometrical dựa trên CRD chức năng chord (đều liên quan đến chức năng của sin sin a = (2 CRD một) / 120). Ptolemy chứng minh mới nghĩ ra hình học và định lý. Ông đã thu được, bằng cách sử dụng Chords của một vòng tròn và một ghi 360-gòn, các xấp xỉ π = 3 17 / 120 = 3,14166 và, bằng cách sử dụng √ 3 = chord 60, √ 3 = 1,73205. Ông đã sử dụng công thức cho các chức năng CRD có công thức tương tự cho tội lỗi của chúng tôi (a + b), sin (a - b) và một tội lỗi / 2 để tạo ra một bảng của hàm CRD sau khoảng 1 / 2 một mức độ. Điều này chiếm đầu tiên hai trong 13 cuốn sách của Almagest và sau đó, trích dẫn lời một lần nữa từ giới thiệu, chúng tôi cung cấp cho Ptolemy mô tả của riêng của ông dự định làm thế nào để phát triển các phần còn lại của thiên văn học toán học vào hoạt động này (xem ví dụ): [Sau khi giới thiệu các khái niệm toán học] chúng tôi đã đi qua những chuyển động của mặt trời và của mặt trăng, và các hiện tượng đi kèm với những chuyển động; cho nó sẽ không thể kiểm tra các lý thuyết của các ngôi sao triệt để mà không có một đầu tiên nắm bắt các vấn đề . Công việc cuối cùng của chúng tôi trong cách tiếp cận được các lý thuyết của những ngôi sao. Ở đây quá nó sẽ là thích hợp nhất để đối phó với các mặt cầu của cái gọi là 'ngôi sao cố định, và sau đó bằng cách xử lý các hành tinh năm' ', khi họ được gọi là. Trong kiểm tra lý thuyết của mặt trời, Ptolemy so sánh các quan sát của riêng ông equinoxes với những người của Hipparchus và các quan sát trước đó Meton trong 432 TCN. Ông khẳng định độ dài của năm nhiệt đới như là 1 / 300 của một ngày ít hơn 365 1 / 4 ngày, giá trị thu được chính xác bởi Hipparchus. Vì, như Ptolemy tự biết, tính chính xác của phần còn lại của dữ liệu của mình phụ thuộc rất nhiều vào giá trị này, thực tế là giá trị thật sự là 1 / 128 của một ngày ít hơn 365 1 / 4 ngày đã sản xuất ra lỗi trong phần còn lại của tác phẩm . Chúng ta sẽ thảo luận chi tiết hơn dưới đây là lời buộc tội đó đã được thực hiện đối với Ptolemy, nhưng điều này minh họa rõ ràng các căn cứ cho những lời buộc tội từ Ptolemy đã phải có một lỗi của 28 giờ trong quan sát của ông về phân để sản xuất ra lỗi này, và thậm chí cho các độ chính xác mà có thể được dự kiến với nhạc cụ cổ xưa và các phương pháp, đó là bản chất unbelievable rằng ông có thể đã thực hiện một lỗi của cường độ này. Một cuộc thảo luận tốt về lỗi này lạ được chứa trong bài viết xuất sắc. Dựa trên những quan sát của ông về solstices và equinoxes, Ptolemy tìm thấy độ dài của các mùa và, dựa trên các, ông đã đề xuất một mô hình đơn giản cho mặt trời mà là một chuyển động tròn của vận tốc góc đồng bộ, nhưng đất đã không được ở trung tâm của vòng tròn, nhưng ở một khoảng cách được gọi là tâm sai từ trung tâm này. Lý thuyết này của mặt trời tạo thành chủ đề của Sách 3 của Almagest. Trong Sách 4 và 5 Ptolemy cho lý thuyết của ông về mặt trăng. Tại đây ông sau Hipparchus người đã nghiên cứu ba giai đoạn khác nhau mà ta có thể kết hợp với sự chuyển động của mặt trăng. Hiện là thời gian thực hiện cho mặt trăng để quay lại cùng kinh độ, thời gian đưa cho nó để trở về cùng một vận tốc (các bất thường) và thời gian đưa cho nó để trở về cùng vĩ độ. Ptolemy cũng thảo luận, như Hipparchus đã làm, tháng synodic, đó là thời gian giữa oppositions tiếp của mặt trời và mặt trăng. Trong Sách 4 Ptolemy cho Hipparchus 's mô hình cho các ngoại luân chuyển động của mặt trăng nhưng ông đã ghi chú, như trong Hipparchus thực tế đã làm chính mình, rằng có sự sai biệt nhỏ giữa các mô hình và các thông số quan sát. Mặc dù ghi nhận những sự trái ngược nhau, Hipparchus có vẻ như không phải làm việc trên một mô hình tốt hơn, nhưng Ptolemy thực hiện điều này trong Sách 5, nơi ông đã mang lại cho mô hình được cải thiện rõ rệt về một đề xuất bởi Hipparchus. Một cuộc thảo luận thú vị của lý thuyết Ptolemy của mặt trăng được cho vào. Có được một lý thuyết cho sự chuyển động của mặt trời và mặt trăng, Ptolemy đã ở một vị trí để áp dụng này để có được một lý thuyết của eclipses mà ông nào trong Sổ 6. Hai cuốn sách kế tiếp đối phó với những ngôi sao cố định và trong Sách 7 Ptolemy sử dụng các quan sát của mình cùng với những người trong Hipparchus để biện minh cho niềm tin của mình rằng những ngôi sao cố định luôn luôn duy trì cùng một vị trí tương đối với nhau. Ông đã viết (xem ví dụ): Nếu được để phù hợp với sắp xếp trên đối với các sơ đồ hình thành các chòm sao trên thiên cầu Hipparchus 's, ông sẽ thấy rằng vị trí của các ngôi sao có liên quan trên toàn cầu do các quan sát được thực hiện tại thời Hipparchus, theo những gì ông đã ghi lại , rất gần giống như hiện nay. Trong các Ptolemy hai cuốn sách cũng bàn về tuế sai, việc phát hiện ra mà ông đã thuộc tính để Hipparchus, nhưng con số này của ông là phần nào do lỗi chủ yếu là do lỗi trong chiều dài của năm nhiệt đới mà ông đã sử dụng. Nhiều Sách 7 và 8 được đưa lên với mục lục sao Ptolemy có chứa hơn một nghìn ngôi sao. Những năm cuối cùng sách của Almagest thảo luận về lý thuyết hành tinh. Điều này phải được thành tựu lớn nhất của Ptolemy về một sự đóng góp ban đầu, kể từ đó không xuất hiện để có được bất kỳ thỏa đáng mô hình lý thuyết để giải thích các chuyển động khá phức tạp của năm hành tinh trước khi Almagest. Ptolemy kết hợp các ngoại luân và phương pháp lập dị để cung cấp cho mô hình của mình cho các chuyển động của các hành tinh. Đường dẫn của một hành tinh P do đó bao gồm chuyển động tròn trên một ngoại luân, C trung tâm của ngoại luân chuyển quanh một vòng tròn trung tâm mà đã được bù đắp từ trái đất. Đổi mới thực sự thông minh Ptolemy ở đây là để làm cho sự chuyển động của C không thống nhất về các trung tâm của vòng tròn xung quanh mà nó di chuyển, nhưng xung quanh một điểm gọi là tâm sai là đối xứng được đặt ở phía đối diện của trung tâm từ trái đất. Lý thuyết hành tinh mà Ptolemy phát triển ở đây là một kiệt tác. Ông đã tạo ra một mô hình toán học phức tạp để phù hợp với các dữ liệu quan sát được thời gian trước khi Ptolemy đã khan hiếm, và mô hình của ông sản xuất, mặc dù phức tạp, đại diện cho các chuyển động của các hành tinh khá tốt. Toomer tiền lập Almagest tại như sau: Như một tác phẩm giáo khoa là "Almagest" là một kiệt tác của sự rõ ràng và phương pháp, cấp trên bất kỳ sách giáo khoa khoa học cổ đại và với các bạn cùng vài từ thời kỳ nào. Nhưng đó là nhiều hơn đó. Xa là một systemisation chỉ "của thiên văn học Hy Lạp trước đó, vì nó là đôi khi được mô tả, đó là ở nhiều khía cạnh một tác phẩm gốc. Chúng tôi sẽ trở lại để thảo luận về một số trong những cáo buộc thực hiện đối với Ptolemy sau khi bình luận ngắn gọn về các tác phẩm khác của ông. Ông đã xuất bản các bảng mà nằm rải rác khắp Almagest riêng theo Handy Tiêu đề Tables. Đây không chỉ đơn thuần nâng lên từ Almagest tuy nhiên nhưng Ptolemy đã cải thiện rất nhiều trong trình bày của mình, dễ sử dụng và ông thậm chí thực hiện cải tiến trong các thông số cơ bản để cung cấp cho hơn độ chính xác. Chúng tôi chỉ biết chi tiết của Bàn Handy thông qua các lời bình luận của Theon Alexandria nhưng trong tác giả cho thấy, chăm sóc được yêu cầu kể từ Theon đã không được nhận thức đầy đủ thủ tục Ptolemy. Ptolemy cũng đã làm những gì nhiều nhà văn sâu sắc của công trình khoa học đã làm, và vẫn làm, bằng văn bản một tài khoản phổ biến của các kết quả của mình theo các hành tinh Tiêu đề Hypothesis này làm việc,. Tại hai cuốn sách, một lần nữa sau các tuyến đường quen thuộc của việc giảm các kỹ năng toán học cần thiết bởi một đầu đọc. Ptolemy thực hiện điều này khá khéo léo bằng cách thay thế các lý thuyết hình học trừu tượng bởi những cơ khí. Ptolemy cũng đã viết một tác phẩm về chiêm tinh. Nó có vẻ lạ để người đọc hiện đại mà một người đã viết các cuốn sách khoa học giỏi nên viết trên chiêm tinh. Tuy nhiên, thay vì Ptolemy thấy nó một cách khác nhau cho các ông tuyên bố rằng Almagest cho phép một để tìm vị trí của các vật thể trên trời, trong khi cuốn sách chiêm tinh của ông thấy như là một công việc đồng hành mô tả tác động của các cơ quan thiên về cuộc sống của người dân. Trong một cuốn sách mang tên Analemma ông đã thảo luận về phương pháp tìm ra các góc cần phải xây dựng một đồng hồ mặt trời có liên quan đến các dự của các điểm trên bầu trời. Trong Planisphaerium ông là có liên quan với các dự stereographic của bầu trời lên một máy bay. Điều này được thảo luận tại nơi nó được nêu rõ: Trong chiếu stereographic được điều trị bằng Ptolemy trong "Planisphaerium hình cầu" thiên thể được ánh xạ lên máy bay của đường xích đạo bằng cách chiếu từ cực nam. Ptolemy không chứng minh là tài sản quan trọng là vòng tròn trên mặt cầu trở thành vòng tròn trên máy bay. Chủ yếu làm việc Ptolemy Địa lý, trong tám cuốn sách, cố gắng bản đồ thế giới biết đến cho tọa độ trong những nơi chính trong điều khoản của vĩ độ và kinh độ. Nó không phải là đáng ngạc nhiên rằng các bản đồ được đưa ra bởi Ptolemy đã khá chính xác ở nhiều nơi để ông có thể không được dự kiến sẽ làm nhiều hơn so với sử dụng dữ liệu có sẵn và điều này là có chất lượng rất kém cho bất cứ điều gì bên ngoài Đế quốc La Mã, và thậm chí cả các phần của La Mã Đế quốc được nghiêm méo. Trong Ptolemy được mô tả là: ... một người đàn ông làm việc [trên bản đồ, xây dựng] mà không có sự hỗ trợ của một lý thuyết phát triển, nhưng trong một truyền thống toán học và hướng dẫn bởi ý thức của mình về những gì là thích hợp cho vấn đề. Một tác phẩm khác trên Optics là trong năm sách và trong nó Ptolemy nghiên cứu về màu sắc, phản chiếu, khúc xạ, và tấm gương của các hình dáng khác nhau. Toomer ý kiến tại: Thành lập các lý thuyết của thử nghiệm, thường xuyên bằng cách xây dựng bộ máy đặc biệt, là một tính năng nổi bật nhất của Ptolemy "Quang học". Cho dù đối tượng là phần lớn nguồn gốc hoặc bản gốc, "The Quang học" là một ví dụ đầy ấn tượng của sự phát triển của một ngành khoa học toán học liên quan do các dữ liệu vật lý, và xứng đáng của các tác giả của "Almagest". Một bản dịch tiếng Anh, cố gắng loại bỏ các điều không chính xác giới thiệu trong bản dịch tiếng Ả Rập nghèo mà là nguồn duy nhất của chúng tôi của Quang được cho vào. Việc đầu tiên để thực hiện lời buộc tội chống lại Ptolemy đã được Tycho Brahe. Ông đã khám phá ra rằng có một lỗi hệ thống của một trong những bằng cấp trong các kinh độ của các ngôi sao trong catalogue ngôi sao, và ông cho rằng, mặc dù Ptolemy nói rằng nó đại diện cho các quan sát của mình, nó đã được chỉ đơn thuần là một sự chuyển đổi của một danh mục do Hipparchus sửa chữa cho tuế sai đến ngày Ptolemy. Có tất nhiên vấn đề xác định so sánh hai catalogue sao, một trong số đó chúng tôi có một bản sao trong khi khác sẽ bị mất. Sau khi có ý kiến của Laplace và Lalande, tiếp theo để tấn công mạnh mẽ Ptolemy đã Delambre. Ông cho rằng có lẽ là lỗi đến từ Hipparchus và Ptolemy có thể đã được thực hiện không có gì nghiêm trọng hơn để có không đúng Hipparchus 's dữ liệu cho thời gian giữa equinoxes và solstices. Tuy nhiên Delambre sau đó đi vào để nói (xem): Ai có thể giải thích tất cả mọi thứ trong một kém thuận lợi nhưng tất cả những cách đơn giản bằng cách từ chối Ptolemy quan sát của các ngôi sao, và equinoxes, và bằng cách tuyên bố rằng ông đã đồng hóa tất cả mọi thứ từ Hipparchus, sử dụng các giá trị tối thiểu của các thứ hai cho chuyển động tuế sai. Tuy nhiên, Ptolemy đã không được mà không ủng hộ ông bằng bất cứ phương tiện và phân tích thêm dẫn đến một niềm tin rằng các cáo buộc thực hiện đối với Ptolemy bởi Delambre đã sai. Boll viết năm 1894 nói: Để tất cả các lần xuất hiện, một sẽ phải Ptolemy với tín dụng cho một hình ảnh phong phú hơn về bản chất của firmament Hy Lạp nổi tiếng sau khi người tiền nhiệm của ông. Vogt cho thấy rõ ràng trong giấy quan trọng của mình rằng bằng cách xem xét Hipparchus 's luận về Aratus và Eudoxus và làm cho các giả định hợp lý rằng các dữ liệu nhất định có đồng ý với Hipparchus' s catalogue sao, sau đó catalogue sao Ptolemy không thể có được sản xuất từ các vị trí của các ngôi sao như được đưa ra bởi Hipparchus, ngoại trừ một số ít các ngôi sao mà Ptolemy không xuất hiện để lấy dữ liệu từ Hipparchus. Vogt viết: Điều này cho phép chúng tôi xem xét các danh mục sao cố định như làm của riêng mình, cũng giống như Ptolemy mình mạnh mẽ tiểu bang. Những cáo buộc mới nhất của giả mạo được thực hiện đối với Ptolemy đến từ Newton tại. Ông bắt đầu cuốn sách này bằng cách nêu rõ quan điểm của mình: Đây là câu chuyện của một tội phạm khoa học. ... Tôi có nghĩa là một tội phạm cam kết của một nhà khoa học đối với đồng bào các nhà khoa học và các học giả, một sự phản bội của đạo đức và liêm chính của nghề nghiệp của ông đã mãi mãi tước nhân loại thông tin cơ bản về một lĩnh vực quan trọng của thiên văn học và lịch sử. Tới cuối Newton, có tuyên bố để chứng minh sự quan sát mọi tranh chấp với Ptolemy trong Almagest được chế tạo, viết: [Ptolemy] phát triển lý thuyết nào đó thiên văn và phát hiện ra rằng họ không phù hợp với quan sát. Thay vì bỏ giả thuyết, ông cố ý chế tạo các quan sát từ các lý thuyết để ông có thể cho rằng các quan sát chứng minh tính hợp lệ của các lý thuyết của ông. Trong mỗi khoa học hoặc học thiết lập được biết, thực hành này được gọi là gian lận, và nó là một tội ác chống lại khoa học và học bổng. Mặc dù các bằng chứng được sản xuất bởi Brahe, Delambre, Newton và những người khác chắc chắn nào cho thấy Ptolemy lỗi là không ngẫu nhiên, điều này báo trước từ được, tôi [EFR] tin rằng, một tội ác chống lại Ptolemy (để sử dụng ngôn từ của Newton). Cuốn sách này được viết để học tập hiệu lực của những lời buộc tội và nó là một công việc mà tôi tin tưởng mạnh mẽ cho việc giải thích đúng. Grasshoff viết: ... đã đến một giả định rằng một tỷ lệ đáng kể những danh mục sao Ptolemy là căn cứ trên những quan sát Hipparchan mà Hipparchus đã được sử dụng cho việc biên soạn phần thứ hai của "ông luận về Aratus". Mặc dù nó không thể cai trị ra rằng tọa độ quả từ những quan sát chính hãng Ptolemy được bao gồm trong danh mục này, họ không thể số tiền để catalogue hơn một nửa. ... sự đồng hóa của các quan sát Hipparchan không còn có thể được thảo luận theo khía cạnh của đạo văn. Ptolemy, có ý định là phát triển một lý thuyết toàn diện về hiện tượng thiên thể, không có quyền truy cập vào các phương pháp đánh giá bằng cách sử dụng dữ liệu có nghĩa là số học mà nhà thiên văn học hiện đại có thể lấy được từ một bộ khác nhau kết quả đo lường, một đại diện, giá trị cần thiết để thử nghiệm một giả thuyết. Vì lý do phương pháp luận, sau đó, Ptolemy đã buộc phải chọn từ một tập các phép đo giá trị một tương ứng tốt nhất để những gì ông đã phải xem xét như là dữ liệu đáng tin cậy nhất. Khi một lựa chọn trực quan giữa các dữ liệu đã không còn có thể ... Ptolemy đã phải xem xét những giá trị là 'quan sát' mà có thể được xác nhận bởi dự đoán lý thuyết. Là một bình luận cuối cùng chúng tôi báo giá các châm chích được chấp nhận bởi nhiều học giả đã được viết bởi Ptolemy tự, và nó xuất hiện trong Book 1 của Almagest, sau đây là danh sách các nội dung (xem ví dụ): Vâng để tôi biết rằng tôi có sinh tử, một sinh vật của một ngày. Nhưng nếu tâm trí của tôi theo lối đi quanh co của các ngôi sao Sau đó, chân tôi không còn phần còn lại trên trái đất, nhưng đứng bởi Zeus tự tôi đi điền của tôi thuốc trường sanh, các món ăn thiêng liêng.

Claudius Ptolemy Claudius Ptolemy (90-168) sinh sống ở Ai Cập nhưng có tổ tiên là người Hi Lạp. Là một nhà toán học, nhà địa lí và nhà thiên văn học, ông là tác giả của một số bộ sách giáo khoa có tác động lớn đối với hệ tư tưởng phương Tây. Vào thế kỉ thứ 2, Ptolemy cho xuất bản cuốn Almagest, một chuyên luận toàn diện về chuyển động của các ngôi sao và hành tinh. Nó giải thích mô hình địa tâm Hipparchus của chuyển động thiên thể, sử dụng các vòng ngoại luân và nội luân trong một lí thuyết địa tâm đặt Trái đất tại trung tâm của hệ mặt trời. Hệ thống Ptolemy này cung cấp những bảng biểu thông tin cho phép dự đoán tiện lợi vị trí của các hành tinh. Ptolemy còn lập danh mục 48 chòm sao, tên của chúng vẫn được sử dụng ngày nay. Các tác phẩm của Ptolemy được giới cầm quyền ủng hộ trong hơn 12 thế kỉ sau đó. Tuy nhiên, mô hình của ông là không đúng, và sau này nó không được sử dụng khi mô hình nhật tâm của hệ mặt trời ra đời. Ngày nay, chúng ta biết rất ít thông tin về cuộc đời của Ptolemy. Mô hình địa tâm của vũ trụ, do nhà khoa học người Hi Lạp Claudius Ptolemy nghĩ ra, đặt vạn vật quay vòng quanh Trái đất. Ảnh: Bartolomeu Velho Thuyết địa tâm

Ptolemy 90-168 Hy Lạp Thiên Văn Học, Toán Học, địa Lý